
|
Читайте также: |
Серед табличних інтегралів є такі:
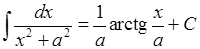 ,
, 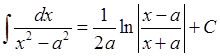 .
.
Покажемо, що до одного з них можна звести інтеграли вигляду:
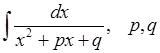 – сталі.
– сталі.
Дійсно, виділимо у знаменнику підінтегрального дробу повний квадрат:
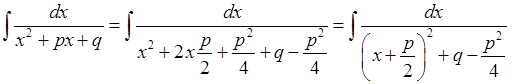
 .
.
Далі можлива одна з 3-х ситуацій.
1)  . Тоді інтеграл набуває вигляду:
. Тоді інтеграл набуває вигляду:
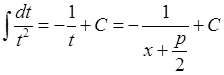 .
.
2) 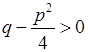 . Тоді, позначивши
. Тоді, позначивши 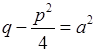 , матимемо:
, матимемо:
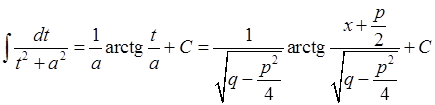 .
.
3) 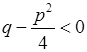 . Тоді, позначивши
. Тоді, позначивши 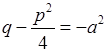 , матимемо:
, матимемо:
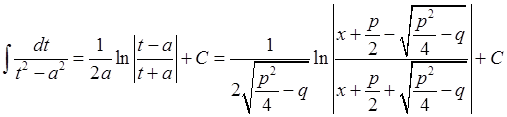 .
.
Зауважимо, що аналогічним чином можна обчислити інтеграли вигляду:
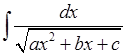 , (6.1)
, (6.1)
зводячи їх до одного з інтегралів:
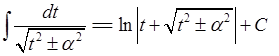 (при
(при 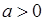 ).
).
 (при
(при 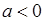 ).
).
Перейдемо до прикладів.
1. 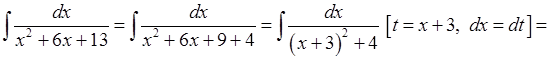
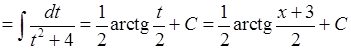 .
.
2. 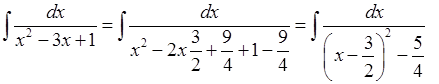
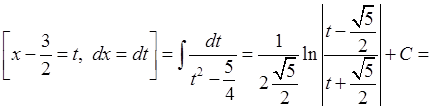
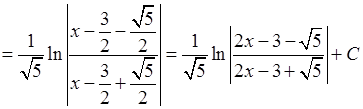 .
.
3. 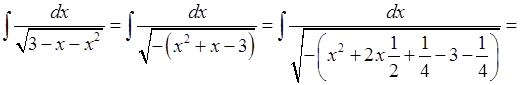
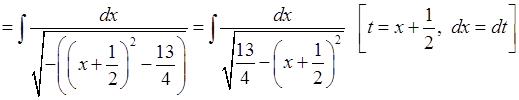
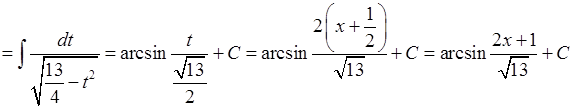 .
.
Розглянемо інтеграл більш загального вигляду:
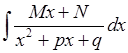 .
.
Виділимо у чисельнику підінтегрального дробу похідну його знаменника:
 .
.
Тоді наш інтеграл набуває вигляду:
 .
.
Перший з цих інтегралів дорівнює 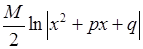 (згідно з формулою (4.2)), а другий обчислюється наведеним вище способом.
(згідно з формулою (4.2)), а другий обчислюється наведеним вище способом.
Аналогічно обчислюються інтеграли вигляду:
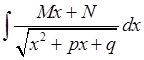 .
.
Їх теж можна розбити на два інтеграли, перший з яких має вигляд:
 , а другий відноситься до вигляду (6.1).
, а другий відноситься до вигляду (6.1).
Розглянемо приклади.
1. 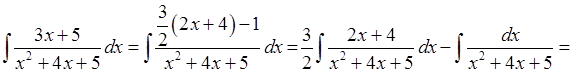
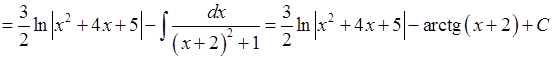 .
.
2. 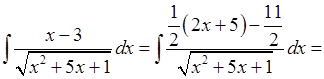
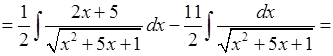
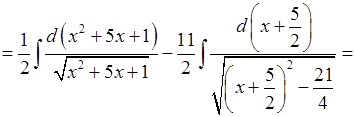

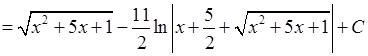 .
.
Інтегрування елементарних дробів.
Елементарними дробами називаються вирази наступного вигляду:
1) 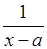 , 2)
, 2) 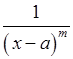 , 3)
, 3) 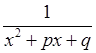 , 4)
, 4) 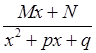 ,
,
5) 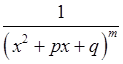 , 6)
, 6) 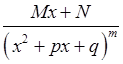 .
.
Тут припускається, що 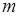 – натуральне число, яке більше 1, а тричлен
– натуральне число, яке більше 1, а тричлен  не має дійсних коренів, тобто його дискримінант
не має дійсних коренів, тобто його дискримінант 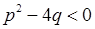 .
.
Розглянемо питання про обчислення інтегралів від цих виразів. Інтеграли від дробів 1), 2) обчислюються дуже просто:

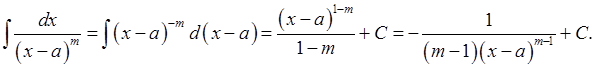
Інтеграли від дробів 3), 4) були розглянуті у п.6. Зосередимось на інтегруванні дробів 5), 6). У п.6 ми бачили, що відповідною заміною змінної інтеграл від дроба 5) можна звести до інтеграла:
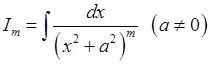 .
.
Тому розглянемо інтеграл  . Застосуємо формулу інтегрування частинами (5.1).
. Застосуємо формулу інтегрування частинами (5.1).
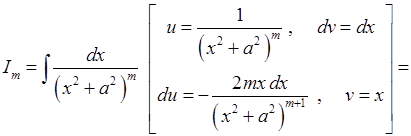
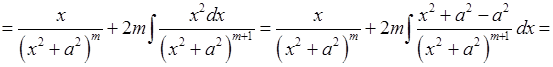
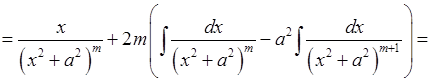
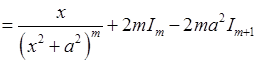 .
.
Звідси:
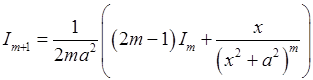 . (7.1)
. (7.1)
Тобто отримали рекурентну формулу, яка дозволяє зводити інтеграл  до інтеграла
до інтеграла  . Зокрема, якщо
. Зокрема, якщо  , то отримуємо:
, то отримуємо:
 .
.
Враховуючи, що
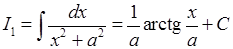 ,
,
маємо:
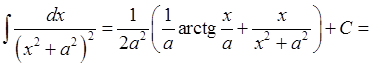
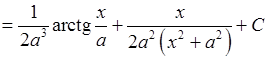 . (7.2)
. (7.2)
Тепер розглянемо інтегрування дробу 6):
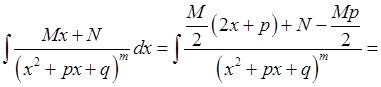

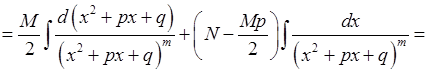
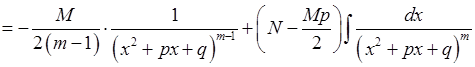 , тобто звели інтеграл до вивченого.
, тобто звели інтеграл до вивченого.
Приклад. Обчислити інтеграл
 .
.
Маємо:
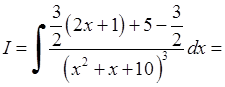
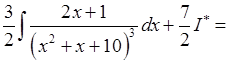
 , де
, де
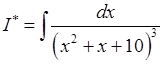 .
.
Обчислимо останній інтеграл окремо.
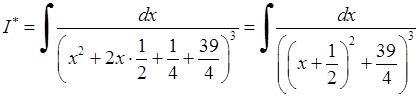
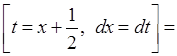
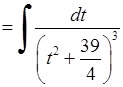 .
.
За формулою (7.1) (при 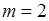 ) маємо:
) маємо:
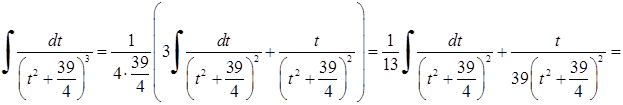
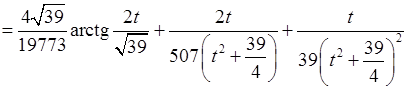 .
.
Отже, повертаючись до змінної 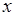 , отримуємо:
, отримуємо:
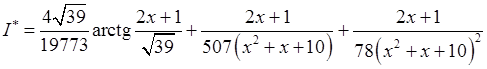 .
.
З урахуванням цього:
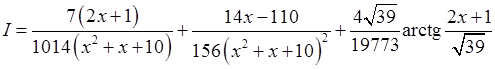 .
.
Дата добавления: 2015-10-30; просмотров: 534 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Диференціала. | | | Інтегрування раціональних функцій. |