Диференціала.

Далеко не всі інтеграли обчислюються так елементарно, як у п.3. Тоді ми змушені використовувати спеціальні методи. Одним з них є метод заміни змінної або метод підстановки. Він ґрунтується на наступній теоремі.

Теорема. Нехай первісна функції на інтервалі , тобто:

, і нехай функція визначена і диференційовна на інтервалі , причому множина значень цієї функції є інтервал . Тоді справедлива формула:

.

Доведення. Згідно з формулою диференціювання складеної функції маємо:

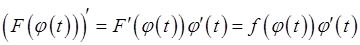, а це означає, що функція є первісною для функції на інтервалі , тобто справедливе твердження теореми.

На практиці метод заміни змінної використовують так. намагаються знайти таку функцію , щоб інтеграл

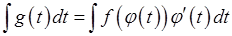був менш складним, ніж початковий інтеграл

.

Часто таку заміну змінної зручно обирати у вигляді , тобто у вигляді залежності від .

На підставі цього метода, зокрема, можна отримати такий результат. Нехай є первісною для функції на інтервалі , тобто

Розглянемо:

(4.1)

Розглянемо приклади.

1).

Цей інтеграл можна було б обчислити безпосередньо, використовуючи формулу бінома Ньютона. Але це досить складно. Помітимо, що цей інтеграл схожий на табличний

.

На підставі формули (7.4.1) маємо:

.

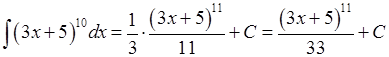Тут .

2). .

Зробимо заміну

Маємо:

.

При обчисленні інтеграла від скористалися формулою (4.1).

Особливо ефективно метод заміни змінної використовується тоді, коли під знаком інтеграла вдається виділити диференціал деякої функції , а решту підінтегрального виразу подати у вигляді складеної функції, де внутрішньою є функція , а саме:

.

Тоді, здійснюючи заміну 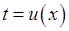, отримуємо інтеграл:

.

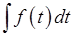Якщо первісна від функції нам відома, то

.

Розглянемо приклади:

1). .

Отже виділили диференціал функції . Зробивши заміну , отримаємо:

.

2). Іноді для виділення диференціалу необхідно підінтегральний вираз помножити (відповідно поділити) на деяку сталу величину.

.

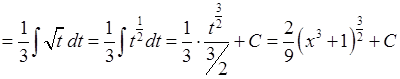3). Важливим є наступний тип інтегралів:

,

тобто у чисельнику підінтегрального дробу міститься диференціал його знаменника. Роблячи заміну 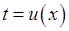, отримуємо інтеграл:

. (4.2)

Тобто інтеграл дорівнює натуральному логарифму модуля знаменника.

Приклади.

1). .

2). .

3). Розглянемо більш складний інтеграл:

.

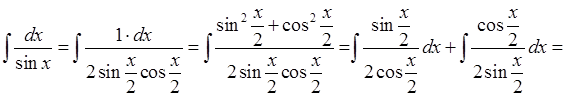
Цей інтеграл можна було б також обчислити за допомогою підстановки .

4).

.

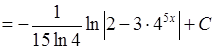Дата добавления: 2015-10-30