Інтегрування раціональних функцій.

Нагадаємо, що раціональною функцією називається функція вигляду:

, де – поліном степеня , а – поліном степеня .

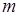Інтеграли від раціональних функцій завжди виражаються через елементарні функції. У деяких випадках до таких інтегралів можна звести інтеграли від інших класів функцій (ірраціональних, тригонометричних). Тому вміння інтегрувати раціональні функції вельми необхідно. Виконання цієї задачі ґрунтується на наступному:

Розглянемо спочатку випадок , тобто степінь чисельника нижче степеня знаменника.

1. Знаменник розкладається на множники, кожен з яких відносить-

ся до одного з наступних чотирьох типів:

I.

II. , де

III. , де

IV. , де

2. Кожному множнику ставиться у відповідність елементарний дріб, або

сума елементарних дробів. А саме:

Множнику I типу ставиться у відповідність дріб .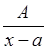

Множнику II типу ставиться у відповідність сума дробів:

.

Множнику III типу ставиться у відповідність дріб .

Множнику IV типу ставиться у відповідність сума дробів:

.

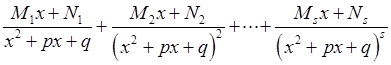Коефіцієнти в чисельниках цих дробів поки що невизначені числа.

3. Підінтегральний дріб записується у вигляді суми всіх цих елемен-

тарних дробів. Потім ця сума приводиться до спільного знаменника, який очевидно співпадає з . Після цього зрівнюються коефіцієнти при однакових степенях 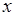у отриманому чисельнику і чисельнику дроба , внаслідок чого отримується система лінійних алгебраїчних рівнянь відносно коефіцієнтів в чисельниках елементарних дробів. Можна показати, що її визначник відмінний від нуля, отже вона має єдиний розв’язок. Розв’язуючи цю систему, підставляємо розв’язок в чисельники елементарних дробів і таким чином зводимо інтегрування раціональної функції до інтегрування елементарних дробів, яке розглянуто у попередньому параграфу.

Нагадаємо, що тут ми припускали, що . Якщо , тобто степінь чисельника вище, або дорівнює степені знаменника, то треба виділити з дроба цілу частину, використовуючи, наприклад, алгоритм ділення стовпчиком. І тоді запишеться у вигляді суми полінома і раціональної функції, степінь чисельника якої вже буде нижче степені її знаменника.

Перейдемо до розглядання прикладів.

Приклади.

1. .

Степінь чисельника співпадає зі степінню знаменника. Виділимо в підінтегральному дробу цілу частину:

.

Тоді:

.

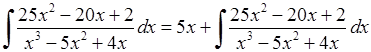Розкладемо на множники знаменник підінтегрального дробу:

.

Звідси бачимо, що всі множники відносяться до I типу. Тому підінтегральний дріб запишеться так:

.

Зводячи тепер суму у правій частині до спільного знаменника, отримуємо:

.

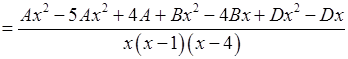Зрівняємо коефіцієнти при однакових степенях 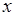в отриманому чисельнику і чисельнику , для чого складемо наступну табличку:

Розв’язуючи цю систему, одержимо: .

Зауважимо, що ці значенні можна було отримати інакше. Оскільки отриманий чисельник співпадає з чисельником для будь яких значень 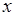, то у рівності

, не розкриваючи дужок, покладемо послідовно . Отримаємо ті ж самі значення для коефіцієнтів .

Іноді є сенс комбінувати обидва методи знаходження коефіцієнтів.

Таким чином маємо:

.

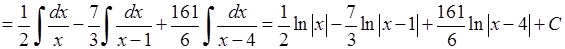Отже

.

2. .

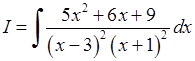Степінь чисельника нижча за степінь знаменника, і у знаменнику два множники II типу. Тому:

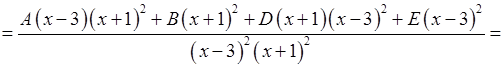
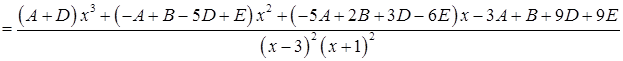
Зрівнюючи коефіцієнти, отримуємо:

Покладаючи і зрівнюючи чисельники, матимемо: .

Покладаючи , отримуємо: .

Звідси 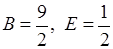, і система спрощується:

.

Звідси . Таким чином маємо:

.

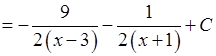3. .

Степінь чисельника вища за степінь знаменника. Виділимо в підінтегральному дробу цілу частину:

.

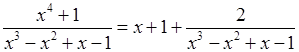Тому

.

Один множник I типу і один множник III типу. Отже

.

Зрівнюючи коефіцієнти, маємо:

Звідси: . І тоді

.

4. .

Степінь чисельника нижча за степінь знаменника, у знаменнику множник I типу, а множник – IV типу. Маємо:

.

Чисельник, що отримується після приведення до спільного знаменника, має вид:

.

Покладаючи тут , одержимо , звідки .

Розкриваючи дужки і зрівнюючи коефіцієнти при однакових степенях 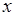, отримаємо наступну систему відносно :

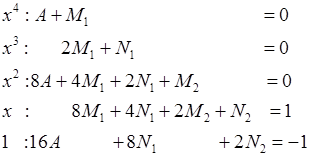
Оскільки вже відомо, що , система легко розв’язується:

З 1–го рівняння: .

З 2–го рівняння: .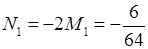

З 3–го рівняння: .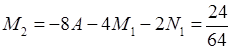

З 4–го рівняння: .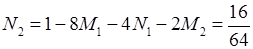

Тепер маємо:

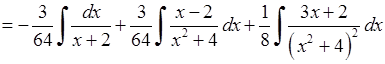. (8.1)

Обчислимо окремо:

;

(скористалися формулою (7.2)).

Підставляючи ці вирази до (8.1), остаточно отримуємо:

.

Дата добавления: 2015-10-30