
Читайте также:
|
Задача 80. Здесь в ходе выполнения инструкции ребята учатся применять понятия, относящиеся к порядку элементов в цепочке, по отношению к русской алфавитной цепочке. Поскольку буквы сравнительно небольшие, некоторым трудно будет их обвести, не задевая соседние буквы. Задевать другие буквы в целом допустимо, но при этом всё-таки должно быть ясно видно, какая буква обведена.
Задача 81. В этой задаче ребята достраивают русскую алфавитную цепочку с помощью инструмента лапка. Наверняка, большинство детей будут восстанавливать цепочку по памяти, повторяя алфавит вслух или про себя. Если вы видите, что слабые учащиеся испытывают при выполнении этой задачи трудности, посоветуйте им использовать в качестве справочного материала цепочку из листа определений.
Задача 82. Как и в предыдущей задаче, здесь вполне допустимо, если кто-то из учащихся будет пользоваться алфавитной цепочкой при решении. Желательно, чтобы ребята использовали алфавитную цепочку при проверке. Особенно полезна будет алфавитная цепочка в тех утверждениях, где приходится отсчитывать буквы от конца цепочки, ведь даже те, кто знает алфавитную цепочку очень хорошо, вряд ли так же хорошо воспроизведут её в обратном порядке.
Задача 83. Словосочетание «буквы стоят в алфавитном порядке» мы будем употреблять в случае, если буквы расставлены в цепочке в том же порядке, в котором они стоят в алфавите. Это означает, что та буква, которая идёт раньше всех остальных в алфавитной цепочке, идёт в цепочке первой, буква, которая идёт раньше из всех оставшихся, идёт второй и т. д. В данной задаче дети работают с наиболее простым набором букв, поэтому пояснения им вряд ли потребуются (однако будьте готовы их дать). Здесь приведены буквы из начального фрагмента алфавитной цепочки, причём буквы даны подряд, без пропусков. Это означает, что данные буквы будут стоять не просто в том же частичном порядке (то есть относительно друг друга), но и на тех же местах, что и в алфавитной цепочке. Первая буква русской алфавитной цепочки — буква А. Она есть в нашем наборе, ставим её в цепочку первой, затем в алфавитной и в нашей цепочке будет стоять буква Б, потом — В и т. д., до тех пор, пока буквы в нашем наборе не закончатся.
Задача 84. В этой задаче дети повторяют алгоритм подсчёта областей картинки. В данном случае картинка довольно затейливая и выделить в ней области визуально оказывается довольно трудно. Тем не менее сильным учащимся эту задачу лучше сначала предложить выполнить на бумаге, а уже после — на компьютере, в качестве проверки.
Задача 85. Здесь учащиеся повторяют понятие «одинаковые цепочки». Поскольку цепочек здесь не много, большинству ребят удастся найти две одинаковые цепочки хаотичным просматриванием.
Задача 86. В этой задаче мы ведём пропедевтику операций над множествами (мешки здесь являются множествами). Знаки, которые необходимо найти и пометить в задаче, составляют пересечение множеств А и Б. Это знаки, которые есть в каждом из двух множеств. В данном случае таких знаков оказывается всего 3. Обратите внимание, в данном случае общие знаки нужно пометить только в мешке А.
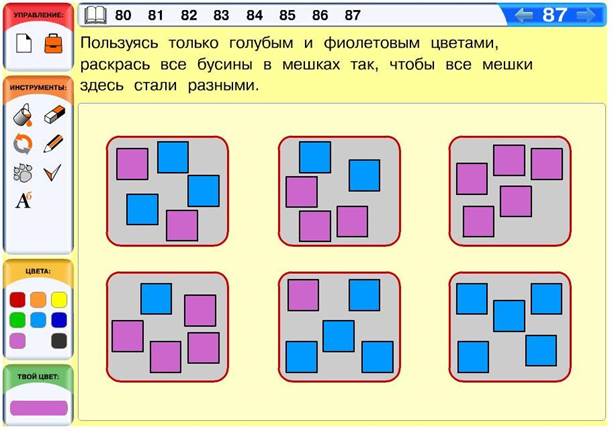
Задача 87 (необязательная). Решение здесь можно построить как методом проб и ошибок, так и используя рассуждения. Действительно, все бусины в каждом мешке должны быть раскрашены в два цвета. Это означает, что бусины, которые не будут раскрашены голубым, нужно будет раскрасить фиолетовым и наоборот. При этом все бусины в мешках одинаковой формы, значит, мешки можно сделать разными только за счёт цветов бусин. Из всего сказанного можно сделать вывод, что мешки будут полностью определяться числом голубых бусин в них, а оно может быть от 0 до 4.
Возможное решение задачи:
Урок «Раньше — позже»
Дата добавления: 2015-10-31; просмотров: 107 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Решение задач 59—67 из учебника | | | Решение компьютерных задач 88—95 |