Производная обратной функции.

Пусть функция y=f (x) монотонна (возрастает или убывает) и непрерывна в некоторой окрестности точки х ₀ и имеет в точке х ₀ производную f¢ (x ₀)≠0. Тогда обратная функция x=j (y) имеет в точке y ₀ =f (x ₀) производную

j ¢(у ₀)= .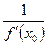

Действительно D y = f (x)- f (x ₀) = у-у ₀ и D х = х-х ₀= j (у)- j (у ₀) = D j, т.е. D у с одной стороны – приращение функции y=f (x), а с другой – приращение аргумента обратной функции x=j (y). Аналогично D х вытекает как приращение аргумента х и как приращение обратной функции. В силу непрерывности обеих функций имеем D y →0 óD х →0, а в силу монотонности D у ≠0óD x ≠0. Учитывая все это, получим

j ¢(у ₀)= = .

Кратко это можно записать так: если y=f (x) и x=х (y) взаимно обратные функции и у¢ ≠ 0, то

х¢=

(18.12)

Пример 18.10. у=arctg x, y=arcsin x. Тогда

(arcsin x)¢=  

(arctg x)¢=

и

Так как x=tg y – обратная к у = аrctg x функция, то по формуле (18.12) получим

y¢=

Вторая формула доказывается аналогично.

Таблица производных

1. (с)¢=0, где с – постоянное число;

2. (х^α)¢= α х^{α- 1}, α Î R, в частности,
х¢ =1, , ;

3. (а^х)¢= а^х ln a, (e^x)¢= e^x;

4. (log _ax)¢= , (ln x)¢= ;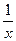

5. (sin x)¢=cos x;

6. (cos x)¢=-sin x;

7. (tg x)¢= = tg² x +1;

8. (ctg x)¢ = -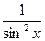

9. (arcsin x)¢ = ;

10. (arccos x)¢ = - ;

11. (arctg x)¢ = ;

12. (arcctg x)¢ = - .

Заметим, что в нашем распоряжении есть полный арсенал средств (таблица производных основных элементарных функций, правила вычисления производных, производная сложной функции) для вычисления производных от элементарных функций.

Дата добавления: 2015-07-20