Читайте также:
|
Функция 
называется бесконечно малой функцией (или просто бесконечно малой, коротко б.м.) в точке 
(при 
), если 
или
(
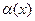- б.м. при ) 
.
Функция 
называется бесконечно большой функцией (или просто бесконечно большой, коротко б.б.) в точке (при ), если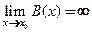 
, т.е. для любой последовательности значений аргумента 
, 
, 
соответствующая последовательность значений функций 
- б.б.:
( - б.б. при ) (
, 
- б.б.).
Определив б.б. функцию, мы фактически дали определение бесконечного предела в точки . Аналогично определяются бесконечные пределы определенного знака: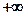 
и 
.
На “языке 
” определение б.б. функции, т.е. бесконечного предела в точке , выглядит так: (
-б.б. при ) 
.
Так, в примере 16.7. мы показали, что многочлен степени 
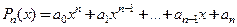является б.б. при 
.
Роль б.м. функций в теории пределов раскрывает следующая теорема.
Теорема 16.4. Функция 
в точке предел, равный А, тогда и только, когда ее можно представить в виде 
, где 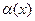- б.м. при . Иными словами:
- б.м. при ).
Доказательство. (Необходимость). Пусть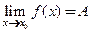 
, положим 
и покажем, что 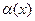- б.м. при . Действительно, для любой последовательности значений аргумента , 
, 
соответствующая последовательность значений функции 
сходится к числу А: 
. Тогда последовательность 
имеет предел при 
, равный нулю: 
. Но “на языке последовательностей” это означает, что 
, т.е. 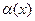- б.м. при .
(Достаточность). Пусть , где 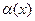- б.м. при . Так как 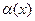- б.м. при , то , т.е.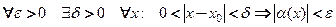 
, т.е. 
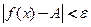. На “языке ” это и означает, что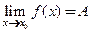
Дата добавления: 2015-07-20; просмотров: 98 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Второй замечательный предел. | | | Основные свойства б.м. функций. |