Основные характеристики поведения функции.

К основным характеристикам поведения функции относятся: нули функции и интервалы знакопостоянства, четность или нечетность, периодичность, монотонность (убывание и возрастание) и экстремумы (максимумы и минимумы), выпуклость или вогнутость и точки

перегиба, ограниченность и наибольшее и наименьшее значения, асимптоты.

Дадим определения некоторых основных характеристик поведения функции, известные из элементарной математики, другие же будем вводить по мере необходимости и расширения арсенала методов исследования.

1. Нули функции. Нулями функции y=f (x) называются корни уравнения f (x) =0, т.е. значения аргумента х, при которых функция обращается в нуль. Другими словами, нуль функции – это точка в которой график функции пересекает ось Ох (см. рис. 15.2.).

х ₁, х ₂– нули функции,

f (x ₁)=0, f (x ₂)=0.

2. Четность, нечетность.

Функция y=f (x), х Î(- а, а) называется четной, если х Î(- а, а)

f (- x)= f (x).

График четной функции симметричен относительно оси Оу (см. рис. 15.3).

Функция y=f (x), х Î(- а, а) называется нечетной если для х Î(- а, а)

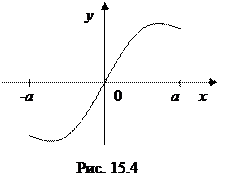f (- x)=- f (x).

График нечетной функции симметричен относительно начала координат (см. рис. 15.4).

Функция может быть ни четной, ни нечетной, т.е. общего вида.

3. Периодичность. Функция y=f (x) называется периодической, если существует такое число а >0, что для любого х справедливо равенство

f (x+а)= f (x).

Наименьшее положительно число а, для которого выполняется вышеприведенное равенство, называется периодом функции и обозначается буквой Т. Тогда х п Î Z

f (x+nT)= f (x).

Поведение периодической функции достаточно изучить на промежутке, длина которого равна периоду функции, например на отрезке [0, T ], где Т – период. График периодической функции получается путем повторения части графика, построенного на отрезке длины, равной периоду функции.

Рассмотрим функцию у=sin x, имеющую период Т =2p. Построив график этой функции на промежутке [-p, p], мы легко распространим его на всю числовую ось (см. рис. 15.5):

Найдем период функции у=sin ax, где а – положительное число. Так как

sin ax=sin (ax +2p) =sin [ a (x+ )],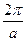

то по определению период функции у=sin x равен 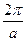, что геометрически означает сжатие графика к оси Оу в а раз при а >1 и растяжение графика от оси Оу при а <1.

4. Монотонные функции. Важными характеристиками поведения функции являются возрастание и убывание.

Функция y=f (x) называется возрастающей в интервале (a, b), если большему значению аргумента соответствует большее значение функции, другими словами, если х ₁, х ₂ Î(a, b)

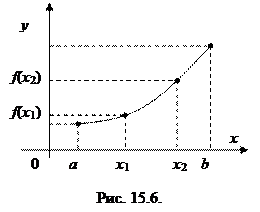
(x ₁< x ₂) => (f (x ₁)< f (x ₂).).

При возрастании аргумента график возрастающей функции поднимается вверх (см. рис. 15.6).

Функция y=f (x) называется убывающей в интервале (a, b), если большему значению аргумента соответствует меньшее значение функции, другими словами, если х ₁, х ₂ Î(a, b)

(x ₁< x ₂) => (f (x ₁)> f (x ₂).).

При возрастании аргумента график убывающей функции опускается вниз (см. рис. 15.7).

На рис. 15.5. изображен график у=sin x. На интервале функция возрастает, а на интервале она убывает.

5. Ограниченность функции.

Ограниченность y=f (x) с областью определения X_f называется ограниченной сверху, если множество ее значений Y_f ограничено сверху, т.е. существует число М такое, что f (x)£ M для х Î X_f. Пусть M_f=sup Y_f – точная верхняя граница значений функции, тогда f (x)£ M_f x Î X_f.

Функция у=f (x), х Î X_f, называется ограниченной снизу, если множество ее значений Y_f ограничено снизу, т.е. существует число m такое, что m £ f (x) х Î X_f. Пусть m_f = inf Y_f – точная нижняя граница значений функции, тогда m_f £ f (x) х Î X_f.

Функция y=f (x) х Î X_f, называется ограниченной, если она ограничена сверху и снизу. В этом случае m_f £ f (x) £ M_f х Î X_f. Условия ограниченности функции f (x) можно записать в следующем виде:

(f (x) ограничена) ó ( M >0 х Î X_f | f (x)| £ М).

В качестве примера рассмотрим функцию y=sin x, ограниченную на всей числовой оси: | sin x | £1, а ее график заключен между прямыми у =±1 (см. рис. 15.5).

Наибольшим значением функции y=f (x), х Î X_f, называется наибольший элемент множества значений Y_f, обозначим его М: М=mах Y_f и найдется значение аргумента x ₁ Î X_f такое, что f (x ₁)= М. Ясно, что тогда М=М_f=sup Y_f.

Наименьшим значением функции y=f (x), х Î X_f, называется наименьший элемент множества значений Y_f, обозначим его m: т=min Y_f и найдется значение аргумента x ₂ Î X_f такое, что f (x ₂)= m. Ясно, что тогда m=m_f=inf Y_f.

Пример 15.1. Рассмотрим функцию у=х ² с областью определения Х_f =[0,1] и областью значений Y_f =[0,1] (см. рис. 15.8а).

Наибольшее значение М= 1= f (1)= M (f), наименьшее значение m= 0= f (0)= m_f.

Если же у =х ² и X_f =[0,1), то Y= [0,1) (см. рис. 15.8б). Тогда, как и выше, функция у=х ² принимает наименьшее значение m =0= f (0)= m_f. Однако наибольшее значение функция не имеет, но ограничена сверху и М_f =1.

Дата добавления: 2015-07-20