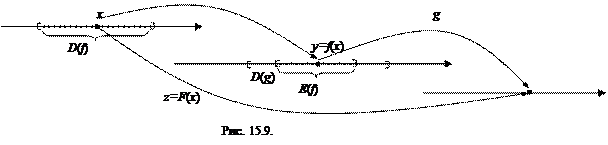Понятие сложной функции.
Числовые промежутки. Окрестность точки. | Индуктивные множества. Натуральные числа. Метод математической индукции. | Понятие числовой последовательности. | Геометрическая прогрессия | Ограниченные и неограниченные последовательности. | Определение предела последовательности. | Бесконечно малые и бесконечно большие последовательности и их свойства. | Арифметические свойства пределов последовательностей | Монотонные последовательности. | Понятия функции. |
Пусть задана функция y=f (x) с областью определения D (f) и множеством значений E (f), а функция z=g (y) определена на множестве D (g), причем E (f)Ì D (g). Тогда на множестве D (f) определена функция z=F (x)= g [ f (x)], которая называется сложной функцией от независимой переменной х (или функцией от функции), а переменная у – промежуточной переменной сложной функции (см. рис. 15.9).
Если, например, z=x 2, а y=sin z, то можно образовать сложную функцию y=sin x 2. Если же z=sin x, а y=z 2, то можно образовать сложную функцию y= (sin x)2= sin 2 x.
Дата добавления: 2015-07-20; просмотров: 112 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.005 сек.)