Монотонные последовательности.

Последовательность { x_n } называется

возрастающей, если x₁ < x₂ < x₃ <... < x_n < x_n+1 <...;

неубывающей, если x₁ x₂ x₃ ... x_n x_n+1 ...;

убывающей, если x₁ > x₂ > x₃ >... > x_n > x_n+1 >...;

неубывающей, если x₁ x₂ x₃ ... x_n x_n+1 ....

Все такие последовательности называется монотонными, а возрастающие и убывающие последовательности называются строго монотонными.

Докажем теорему Вейерштрасса, основную теорему о монотонных последовательностях.

Теорема 14.10. 1) Всякая монотонно возрастающая (неубывающая) и ограниченная сверху последовательность имеет предел.

2) Всякая монотонно убывающая (невозрастающая) и ограниченная снизу последовательность имеет предел.

Доказательство. Докажем первое утверждение. Пусть последовательность { x_n } не убывает, x_n x_n+1 nÎ N, и ограничена сверху. Всякое ограниченное сверху числовое множество имеет точную верхнюю границу (верхнюю грань) a = sup { x_n: nÎ N } и x_n a nÎ N.

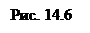
Какое бы положительное число e мы не взяли, число a - e не является верхней границей последовательности { x_n }, т.е. существует номер n₀ такой, что a -e < (см. рис. 14.6). Тогда, учитывая, что последовательность { x_n } неубывающая, для всех n>n₀ имеем a -e < < x_n a <a+ e.

Итак, e >0 n₀ n>n₀ a - e < x_n < a+e, т.е. < e, а это означает, что число a является пределом последовательности { x_n }.

Теорема доказана.

Пример 14.11. Показать, что 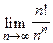= 0.

Решение. Покажем сначала, что последовательность с общим членом x_n = убывает и ограничена снизу.

Действительно, x_n+1 = , тогда 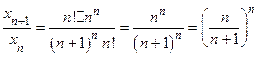<1, т. к. 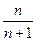<1, отсюда получаем 0< x_n+1 < x_n. Последнее неравенство и означает, что последовательность с общим членом x_n = монотонно убывает и ограничена снизу и по теореме 14.10 имеет предел. Пусть ; ясно, что .

Покажем, что a=0. Предварительно покажем, что >2, т. е. 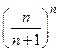< 1/2. Для доказательства воспользуемся формулой бинома Ньютона:

Итак, 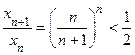или 0 < x_n+1 < 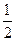x_n.

Перейдем к пределу в последнем неравенстве: или 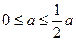. Но это возможно только при a = 0. Неравенство доказано.

Аналогично доказываются следующие важные пределы:

, где q > 1,

, где q > 1, k Î N.

Пример 14.12. Покажем, что последовательность с общим членом сходится и .

Решение. Ясно, что >1. Покажем, что последовательность a_n = -1, a_n>0, является б.м. Это и будет означать, что число 1 является пределом рассматриваемой последовательности. Действительно,

a_n, 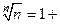a_n, n = (1+ a_n)ⁿ = ,

отсюда или . Окончательно получаем 0 < a_n < . Так как последовательность b_n = – б. м., то, согласно следствию из теоремы о трех последовательностях, a_n тоже б. м. последовательность. Это показывает, что .

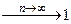Аналогично: =1, а > 0.

В заключении этого пункта приведем важную для дальнейшего так называемую лемму о вложенных отрезках.

Мы говорим, что задана последовательность { I_n } вложенных друг в друга отрезков I_n = [ a_n,b_n ], a_n < b_n, I_n+1 Ì I_n, если a_n a_n+1 < b_n+1 a_n (см. рис. 14.7).

Теорема 14.11. (Лемма о вложенных отрезках).

Пусть последовательность { I_n } вложенных отрезков такова, что 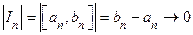. Тогда существует единственная точка сÎR, принадлежащая всем отрезкам: cÎ [ a_n,b_n ] " nÎN.

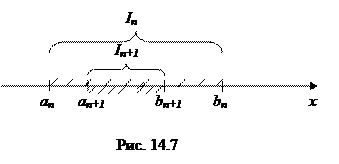Доказательство. Пусть C = { a_n: nÎN } – множество всех левых концов отрезков последовательности { I_n }, а U = { b_n: nÎN }– множество всех правых концов. Из определения последовательности вложенных отрезков вытекает, что a_n < b_m " n, mÎ N и по аксиоме непрерывности множества действительных чисел существует точка c: a_n c b_m " n, mÎ N,в частности, a_n c b_п " nÎ N, т.е. точка c принадлежит всем отрезкам I_n. Покажем, что эта точка – единственная их общая точка. Так как a_n < b_m " n, mÎ N, то

a_n < b₁. Это означает, что последовательность { a_n } левых концов отрезков монотонно возрастает и ограничена сверху, а значит имеет предел , ясно, что a_n с₁.

Последовательность { b_n } правых концов всех отрезков монотонно убывает и ограничена снизу и имеет предел , . Так как a_n < b_п, то и
[ c₁ , c₂ ] Ì [ a_n, b_n ] " nÎ N. Тогда . Так как последовательность a _п = b_n – a_n – б. м. (см. условие теоремы), то c₂ – c₁ = 0 и с₁ = с₂ = с.

Теорема доказана.

14.9. Число e.

В этом пункте введем число e, играющее важную роль в математике и ее приложениях.

Рассмотрим последовательность { x_n } c общим членом x_n = 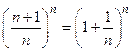. Покажем, что эта последовательность ограничена и монотонно возрастает, следовательно, имеет предел.

Действительно,

x_n = > 2,

т.е. последовательность { x_n } ограничена снизу: 2 x_n " nÎ N. Далее

и х_п =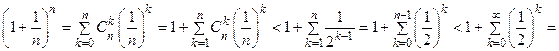

= 1+ 1+2 = 3.

Итак, рассматриваемая последовательность ограничена: 2< х_п < 3, " nÎ N.

Покажем, что эта последовательность монотонно возрастает. Действительно,

,

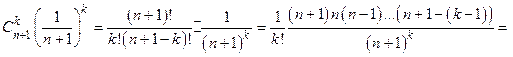
1- .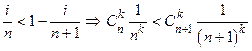

Сравнивая соответствующие слагаемые следующих формул:

x_n =

x_n+1 = ,

мы видим, что х_п < х_п+1, т.е. последовательность возрастает и ограничена сверху. По теореме 14.10 эта последовательность имеет предел, называемый числом e:

, (14.3)

где 2 < e < 3. Без доказательства приведем формулу

или , позволяющую вычислить число e с любой степенью точности. При n = 6 e 2,718.

Замечание. При доказательстве ограниченности последовательности x_n = мы воспользовались формулой суммы бесконечно убывающей геометрической прогрессии. Если x₁, х₂,..., х_п,... – бесконечно убывающая геометрическая прогрессия: x_n+1 = x_nq, где , то

.

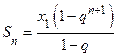Как известно, , поэтому .

Дата добавления: 2015-07-20