Действительные числа.

В школьном курсе математики изучаются действительные (вещественные) числа.

Сначала из потребностей счета возникает натуральный ряд чисел N = {1, 2, 3, …, n, …}, его члены называются натуральными числами. В множестве натуральных чисел определен строгий порядок: из двух натуральных чисел то, которое в натуральном ряде появляется раньше, называется меньшим, второе число – большим. В множестве натуральных чисел определены две операции: сложение и умножение натуральных чисел.

Однако операции вычитания и деления не всегда выполнимы в множестве натуральных чисел N. Поэтому расширение понятия числа пошло в двух направлениях. Возникают отрицательные числа и число ноль, т.е. возникает множество целых чисел Z = {0, ±1, ±2, …, ± n,…}.

Необходимость рассмотрения частей целого приводит к появлению долей единицы и дробных чисел , где m, n Î N. В итоге этих расширений понятия числа возникает множество рациональных чисел

Q= { : m Î Z, n Î N }.

Это множество обладает, в отличие от множеств N и Z, тем свойством, что оно замкнуто относительно арифметических операций сложения и вычитания, умножения и деления: сумма и разность, произведение и частное двух рациональных чисел снова является рациональным числом. Всякое рациональное число единственным образом может быть представлено как бесконечная десятичная периодическая дробь.

С другой стороны, извлечение корня любой степени не всегда возможно в области рациональных чисел, в частности, нет рационального числа, квадрат которого равен 2. этот недостаток рациональных чисел восполняют иррациональные числа, т.е. бесконечные десятичные непериодические дроби, например

= 1,414213562…; π = 3,141592654; е = 2,718281828….

Иррациональные числа нельзя представить в виде отношения , где m Î Z, n Î N.

Рациональные и иррациональные числа (бесконечные десятичные периодические и непериодические дроби) образуют множество действительных чисел R; при этом

N Ì Z Ì Q Ì R.

На действительные числа переносятся действия сложения и вычитания, умножения и деления, возведения в степень и извлечение корня n -ой степени, n Î N, из положительного числа и т.д., в частности, отношение порядка: про любые два действительные числа можно сказать, какое из них больше, а какое меньше.

Геометрически действительные числа изображаются точками числовой оси или координатной прямой (т.н. процесс десятичного измерения отрезка прямой).

Рассмотрим прямую с выбранным на ней направлением, начальной точкой О и единичным отрезком ОЕ (см. рис. 13.2). С помощью отрезка ОЕ можно измерить длину любого отрезка, например, отрезка ОА.

О

Рис. 13.2

Отрезок ОЕ укладывается в отрезке ОА три раза (это целая часть числа). Разделим единичный отрезок ОЕ на 10 равных частей и отложим десятую часть отрезка ОЕ в остатке ВА два раза. Тогда число 3,2 есть приближенное значения длины отрезка ОА с точностью до 0,1. Продолжая этот процесс, мы получим десятичную дробь, выражающую длину отрезка ОА. Полученная десятичная дробь есть действительное число, а точка А изображает число на числовой оси. Числовая ось есть не что иное, как линейка.

В современной математике принят аксиоматический теоретико-множественный подход к понятию действительного числа. Дадим основное определение.

Множество R называется множеством действительных чисел, если оно удовлетворяет следующим условиям (аксиомам):

(I). Операция сложения.

Для каждых двух чисел x Î R и у Î R определено число х+у Î R, называемое их суммой, при этом выполняются аксиомы сложения:

1₊ (х+у)+ z=x+ (y+z),

2₊ x+y=y+x,

3₊ число ноль, 0Î R, такое, что х Î R (x+ 0=0+ x=x),

4₊ х Î R противоположное (– х)Î R, такое, что х+ (– х)=(– х)+ х =0.

(II). Операции умножения.

Для каждых двух чисел x Î R и у Î R определено число х • у Î R, называемое их произведением, при этом выполняются аксиомы умножения:

1_´ (х•у)• z=x• (y•z),

2_´ x•y=y•x,

3_´ число 1Î R, 1≠0, называемое единицей, такое, что х Î R 1• х = х• 1= х,

4_´ х Î R, х ≠0, обратное число х ^-1Î R такое, что х• х ^-1= х ^-1• х= 1

(I, II). Связь сложения и умножения.

(Дистрибутивность умножения по отношению к сложению)

(х+у) z = xz+yz

(III). Отношение порядка.

На множестве R определено отношение неравенства ≤, при этом выполняются аксиомы неравенства:

1_≤ х ≤ х х Î R (рефлексивность);

2_≤ (х ≤ у) 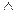(y ≤ x) => (x=y), (антисимметричность);

3_≤ (х ≤ у) 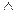(y ≤ z) => (x ≤ z), (транзитивность);

4_≤ Для каждых двух чисел x Î R и у Î R выполняется одно из двух условий:

(х ≤ у) 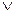(y ≤ x).

(I, III). Связь сложения и порядка.

(х ≤ у) => (x+z ≤ y+z).

(II, III). Связь умножения и порядка.

(0≤ х) 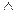(0≤ y) => (0≤ xy).

(IV). Полнота (непрерывность) действительных чисел

Если Х и Y - непустые подмножества множества R, т.е. Х Ì R, X ≠ Ø, Y Ì R, Y≠Ø, и х Î X y Î Y x ≤ y.

Тогда найдется число с Î R такое, что х Î X y Î Y

x ≤ с ≤ y.

В теории множеств доказывается, что вышеприведенные аксиомы однозначно определяют объект, называемый множеством действительных чисел, и что ранее построенное множество R есть конкретная реализация аксиоматики действительных чисел.

Некоторые следствия из аксиом:

1. Разность чисел. По определению: а–b=a+ (-b);

2. Обратный элемент. По определению: а^{- 1}= ;

3. х• 0=0 х Î R;

(х у= 0) => (х = 0) 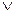(у = 0).

4. Строгое неравенство. По определению

(х<y) ó (x ≤ y) 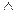(x≠y).

Для каждых двух чисел х Î R и y Î R выполняется только одно из неравенств:

х < y, x = y, x > y

В частности, 0<1 и х>y> 0 => < .

5. Принцип Архимеда: а Î R n Î N: n>a.

1) а> 0 b >0 n Î N: na>b,

2) ε> 0 n Î N: 0< < ε,

3) если 0≤ х < n Î N, то х =0.

6. Абсолютная величина числа: | х | = .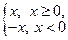

Некоторые ее свойства:

| а |³0, | а+b |≤| a |+| b |, | ab |=| a |•| b |, .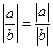

Второе неравенство называется неравенством треугольника.

Расстояние между числами: r (х, у) = | х–у |.

Дата добавления: 2015-07-20