Метод Гаусса решения СЛАУ.

Метод Гаусса решения систем линейных уравнений (метод исключения переменных) основан на том, что элементарные преобразования уравнений (перемена уравнений местами, умножения уравнения на отличное от нуля число, прибавление к одному уравнению другого уравнения, умноженного на число) приводят к эквивалентным системам.

Алгоритм метода Гаусса

Шаг 1. Пусть а ₁₁≠0 (этого можно добиться перестановкой уравнений).

Обозначим через Y_i, i =1, …, m i -ое уравнение системы (11.1). исключим из 2-го, …, m -го уравнений системы переменную х ₁ с помощью элементарных преобразований вида
Y_i- Y ₁, i =2, …, m. Получим эквивалентную систему

(11.10)

Шаг 2. а ≠0. Применим шаг 1 к подсистеме системы (11.10), составленной из 2-го, …, m -го уравнений и исключим переменную х ₂ из 3-го, …, m -го уравнений.

Продолжая этот процесс, после (r- 1)-го шага получим ступенчатую систему вида

(11.11)

Если среди чисел , …, есть отличные от нуля, то система (11.11), а следовательно и исходная система (11.1), несовместна.

Если =…= =0, то система совместна и возможны два случая:

1) r = n, т.е. система примет вид

(11.12)

Так как а ₁₁≠0, ≠0, …, ≠0, то определитель этой системы отличен от нуля, система невырожденная и имеет единственное решение.

2) r < n, систему (11.11) можно представить в виде

(11.13)

Из этой системы перемещения х ₁, …, х_r единственным образом выражаем через переменные х_{r+ 1}, …, x_n. Решений бесконечное множество.

Приведение системы (11.1) к виду (11.11) или (11.13) называется прямым ходом метода Гаусса, а нахождение переменных х ₁, …, х_r из системы (11.13) называется обратным ходом метода Гаусса.

В заключении отметим, что указанные преобразования системы (11.1) равносильны соответствующим преобразованиям расширенной матрицы системы (11.3)

Тогда метод Гаусса запишем в виде

Прямой ход

Обратный ход

Замечание. Метод Гаусса позволяет решать одновременно по несколько СЛАУ с общей матрицей системы.

11.4 Исследование СЛАУ: Терема Кронекера-Капелли.

Рассмотрим произвольную систему линейных уравнений

(11.14)

и матрицу А и расширенную матрицу системы: А= , = .

Центральной в теории систем линейных уравнений является

Теорема 11.1. (Кронекера-Капелли). Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы:
rang A=rang .

Доказательство: 1) Необходимость. Пусть система совместна, т.е. числа с ₁, …, с _n, обращающие каждое уравнение системы в верное равенство:

Перепишем эти равенства в векторной форме с помощью вектор-столбцов матрицы А:

с ₁ А ¹+ с ₂ А ²+ …+ с_nАⁿ = .

Последнее равенство показывает, что вектор- столбец свободных членов является линейной комбинацией вектор- столбцов матрицы А, т.е. вектор-столбец свободных членов не влияет на вычисление ранга матрицы : r (A)=r().

Достаточность. Пусть r (A)=r(). Возьмем какой-нибудь базисный минор матрицы А (он же базисный минор расширенной матрицы ). Тогда вектор-столбцы матрицы А, образующие базисный минор, образуют базис в системе всех вектор- столбцов матрицы , в частности, вектор- столбец свободных членов является линейной комбинацией базисных вектор- столбцов.

Пусть r (A)=r()= r и М 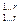- базисный минор, тогда найдутся числа с ₁, …, с_r такие, что

= с ₁ А ¹+ …+ с_rА^r = с ₁ А ¹+ …+ с _r А ^r + 0•А^{r+ 1} …+ 0•Аⁿ.

Последнее равенство и означает, что вектор (с ₁, …, с_r, 0, …, 0) дает решение исходной системы и система совместна. Доказательство окончено.

Теорема Кронекера-Капели, давая ответ на вопрос о совместности системы, позволяет исследовать структуру решения системы.

Пусть система совместна: r (A) = r(). Выберем какой-нибудь базисный минор матрицы А, для определенности считаем, что это М 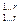, где r=r (А) и М 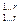≠0..

Из теоремы о базисном миноре вытекает, что уравнение системы с номерами r+ 1, …, n, и является следствием первых r уравнений. Поэтому система (7.14) можно переписать в виде

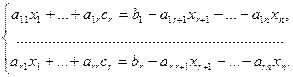(11.15)

Определитель этой системы- минор М 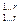≠0, поэтому переменные х ₁, …, х_r единственным образом выражается через переменные х_{r+ 1}, …, x_n (например, по формулам Крамера). Получим общее решение системы:

(11.16)

Введем некоторые определения. Переменные, образующие базисный минор, называются базисными (зависимыми), остальные переменные- свободными (независимыми).

Если выбрать какой-либо базисный минор и положить соответствующие свободные переменные равными нулю, то получится решение системы, называемое базисным. Базисных решений столько, сколько базисных миноров имеет матрица системы А.

Поясним, что означает термин «общее решение системы». Это означает, что любое решение системы можно получить из равенств (11.16) соответствующим выбором свободных переменных.

Дата добавления: 2015-07-20