Окружность.

Окружностью называется множество всех точек плоскости, находящихся на одинаковом расстоянии R от заданной точки О.

Точка О называется центром, а R - радиусом окружности.

Введем прямоугольную систему координат Оху, поместив начало системы координат в центр окружности (см. рис. 9.1). Пусть М(х;у) - произвольная точка окружности | ОМ |= R, а | ОМ |= 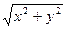. Тогда получим уравнение 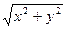= R. Возведя обе части этого уравнения в квадрат, получим каноническое уравнение окружности

	х^2+у^2=R^2

(9.1)

Уравнение (9.1) есть уравнение окружности с центром в начале координат и радиуса R.

Если центр окружности помещен в точку С(х ₀; у ₀ ) (см. рис. 9.2), то уравнение окружности радиуса R с центром в точке
С(х ₀; у ₀ ) имеет вид

	(х-х 0 ) ^2+ (у-у 0 ) ^2= R ^2

(9.2)

Эллипс

Рассмотрим на плоскости две точки F ₁ и F ₂, расстояние между которыми 2 с, и число а>c.

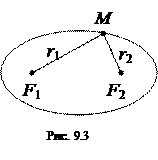Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух данных точек F₁ и F₂, называемых фокусами, есть величина постоянная, равная 2а, т.е.

	r 1 + r 2=2 а

(9.3)

где r ₁ =| F ₁ M | и r ₂= | F ₂ M |- фокальные радиусы произвольной точки М эллипса (см. рис. 9.3).

Для получения уравнения эллипса введем систему координат Оху следующим образом: ось Ох проведем через фокусы эллипса от точки F ₁ к точке F ₂, а начало системы координат точку О поместим в середину круга F ₁ F ₂ (см. рис. 9.4). Тогда фокусы F ₁ и F ₂ получают координаты F ₁ (-с; 0) и F ₂ (с; 0). Если М (х; у) произвольная точка эллипса, то r ₁ =| F ₁ M |= , и r ₂= | F ₂ M |= .

Подставляя r ₁ и r ₂ в равенство(9.3), получим

Приведем это уравнение эллипса к более простому виду.

= 2 а- ,

х²+ 2 сх+с²+у²= 4 а²- 4 а + х²-

- 2 сх+с²+у²,

а =а²-сх,

а²х²- 2 а²сх+ а²с²+а²у²=а⁴- 2 а²сх+с²х²,

(а²-с²)х²+а²у²=а²(а²-с²).

а²-с²=b²

Введем число b >0, положив.

Тогда b²x²+a²y²=a²b².

Разделив последнее уравнение на a²b², получим каноническое уравнение эллипса

	а^2-с^2=b^2

(9.4)

Числа а и b называются большой и малой полуосями эллипса (см. рис. 9.4).

Из уравнения (9.4) вытекает, что эллипс симметричен как относительно координатных осей Ох и Оу, так и относительно начала координат О(0;0) - центра эллипса.

Эксцентриситетом эллипса называют число

, (9.5)

где ε («эпсилон») удовлетворяет условию: 0<ε<1.

Выясним геометрический смысл ε. Из соотношения, связывающего а, b и с, получим

= = , т.е. = .

Теперь ясно, что эксцентриситет характеризует форму эллипса: при уменьшении ε эллипс по форме приближается к окружности, при ε=0 будет b=a и эллипс превращается в окружность; при ε=1 эллипс вырождается в отрезок F₁F₂.

Дата добавления: 2015-07-20