
Читайте также:
|
Рассмотрим две плоскости  и
и  . Взаимное расположение этих плоскостей полностью характеризуется взаимным
. Взаимное расположение этих плоскостей полностью характеризуется взаимным
расположением их нормальных векторов  1={ А 1; В 1; С 1} и
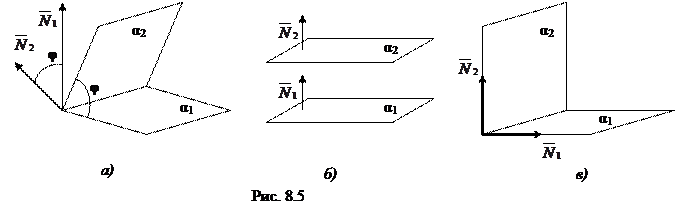
1={ А 1; В 1; С 1} и  2={ А 2; В 2; С 2}. В частности, угол φ между плоскостями равен углу между их нормальными векторами (см. рис. 8.5а) и
2={ А 2; В 2; С 2}. В частности, угол φ между плоскостями равен углу между их нормальными векторами (см. рис. 8.5а) и  .
.
Условие параллельности плоскостей (см. рис. 8.5 б):
α1|| α2 ó  ||
|| 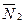 ó
ó 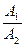 =
= 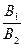 =
= 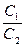 .
.
Условие ортогональности плоскостей (см. рис. 8.5 в)
α1  α2 ó
α2 ó 

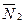 ó А 1 А 2+ В 1 В 2 +С 1 С 2= 0.
ó А 1 А 2+ В 1 В 2 +С 1 С 2= 0.
Дата добавления: 2015-07-20; просмотров: 93 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Нормальное уравнение плоскости. | | | Векторное уравнение прямой. |