Взаимное расположение прямой и плоскости. Перпендикулярность прямой и плоскости.

Признак перпендикулярности прямой и плоскости

Аксиома. Если прямая проходит через две точки данной плоскости, то она лежит в этой плоскости.

Следствие. Если прямая не лежит в данной плоскости, то она имеет с ней не более одной общей точки.

Поэтому для взаимного расположения прямой и плоскости возможны три случая:

1) Прямая лежит в плоскости.

2) Прямая имеет с плоскостью только одну общую точку.

3) Прямая не имеет с плоскостью общих точек.

Прямая называется перпендикулярной плоскости, если она пересекает эту плоскость и перпендикулярна ко всякой прямой в этой плоскости, проходящей через точку пересечения.

· Пучок плоскостей — все плоскости, проходящие через линию пересечения двух плоскостей. Уравнение пучка плоскостей, то есть любой плоскости, проходящей через линию пересечения двух плоскостей, имеет вид:

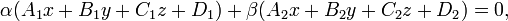
где 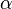и — любые числа, не равные одновременно нулю. Уравнение самой этой линии можно найти из уравнения пучка, подставляя α=1, β=0 и α=0, β=1.

· Связка плоскостей — все плоскости, проходящие через точку пересечения трёх плоскостей. Уравнение связки плоскостей, то есть любой плоскости, проходящей через точку пересечения трёх плоскостей, имеет вид:

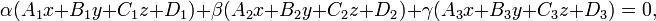
где 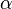, и — любые числа, не равные одновременно нулю. Саму эту точку можно найти из уравнения связки, подставляя α=1, β=0, γ=0; α=0, β=1, γ=0 и α=0, β=0, γ=1 и решая получившуюся систему уравнений.

В заданной плоскости пучком прямых с центром в точке М₀ называют множество всех прямых, лежащих в плоскости и проходящих через точку М₀.

Из определения пучка прямых следует, что любые две прямые заданного пучка прямых пересекаются в точке, которая является центром пучка прямых.

Пучок прямых однозначно определяется, если указан центр этого пучка прямых или две различные прямые этого пучка, что по сути одно и то же.

Уравнение пучка прямых – решение задач.

При решении задач используется не столько сам пучок прямых, сколько уравнение пучка прямых. Другими словами, пучок прямых обычно рассматривается относительно введенной прямоугольной системы координат Oxy на плоскости.

Пусть на плоскости зафиксирована прямоугольная система координат Oxy и указаны две пересекающиеся прямые a₁ и a₂, которые задают пучок прямых. Будем считать, что первой прямой во введенной прямоугольной системе координат Oxy отвечает общее уравнение прямой вида , а второй – вида . Обозначим точку пересечения указанных прямых как M₀, а ее соответствующие координаты как x₀ и y₀. Таким образом, центр пучка прямых есть точка .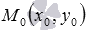

Сформулируем и докажем теорему, которая определяет вид уравнения пучка прямых.

Теорема.

Прямая входит в пучок прямых, который в прямоугольной системе координат Oxy на плоскости задают две пересекающиеся прямые a₁ и a₂, общие уравнения которых имеют вид и , тогда и только тогда, когда ей соответствует общее уравнение прямой вида 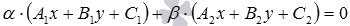, где и - некоторые действительные числа, одновременно не равные нулю (то есть, ).

Дата добавления: 2015-07-25