
Читайте также:
|
Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями.
1. Прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые.
2. Прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются.
3. В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны).
Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются.
На рис. 26 прямая a лежит в плоскости  , а прямая с пересекает
, а прямая с пересекает  в точке N. Прямые a и с — скрещивающиеся.
в точке N. Прямые a и с — скрещивающиеся.
Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой.

На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость  || b (в плоскости
|| b (в плоскости  указана прямая a1 || b).
указана прямая a1 || b).
Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты.
Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

| a || b (прямая а параллельна прямой b) прямая с и прямая а не параллельны прямая с и прямая b не параллельны |
| рис. 8 |
Теорема о параллельных прямых. Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.

| M 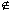 a b||а и М a b||а и М  b (b - единственная) b (b - единственная)
|
| рис. 9 |
Определение. Два отрезка называются параллельными, если они лежат на параллельных прямых.

| отрезок СD || отрезку АВ |
| рис. 10 |
Дата добавления: 2015-07-25; просмотров: 139 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 19 | | | Свойства параллельных прямых |