
Читайте также:
|
Основные понятия.
Определение. Вектор - направленный отрезок, его характеристики- направление и длина.
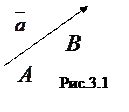 Обозначать вектор будем символом
Обозначать вектор будем символом 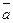 , либо
, либо 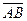 , где точка А – начало вектора, а точка В – конец вектора:
, где точка А – начало вектора, а точка В – конец вектора:

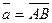 .
.
Начало вектора называется его точкой приложения. Модуль (длину) вектора будем обозначать символом 
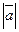 или
или 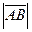 .
.
Векторы 
 и
и  называются коллинеарными, пишем
называются коллинеарными, пишем 
 ||
||  , если они лежат на параллельных прямых.
, если они лежат на параллельных прямых.
 Если коллинеарные векторы сонаправлены (одинаково направлены), то пишем:
Если коллинеарные векторы сонаправлены (одинаково направлены), то пишем: 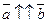 (рис. 3.2 а), если противоположно направлены, то пишем
(рис. 3.2 а), если противоположно направлены, то пишем 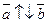 (рис. 3.2 б).
(рис. 3.2 б).
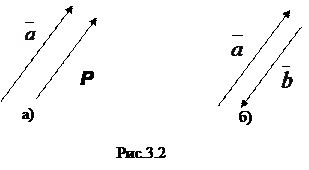 Два вектора
Два вектора  и
и  называются равными, пишем
называются равными, пишем  =
=  , если они сонаправлены и имеют одинаковую длину, т.е.
, если они сонаправлены и имеют одинаковую длину, т.е.
 =
=  <=>
<=> 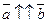 и
и 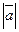 =
= 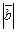
Из этого определения вытекает, что векторы допускают параллельный перенос, т. е. являются свободными, точка приложения вектора может быть выбрана произвольно, а равные векторы совмещаются параллельным переносом.
Нулевой вектор  - вектор, длина которого равна нулю:
- вектор, длина которого равна нулю: 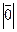 =0. Начало и конец нулевого вектора совпадают, а его направление не определено. Нулевой вектор коллинеарен любому вектору.
=0. Начало и конец нулевого вектора совпадают, а его направление не определено. Нулевой вектор коллинеарен любому вектору.
Единичный вектор или орт - это вектор, длина которого равна единице, если 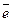 - орт, то
- орт, то
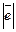 =1. Единичный вектор, сонаправленный с вектором
=1. Единичный вектор, сонаправленный с вектором  , называется ортом вектора
, называется ортом вектора  и
и
обозначается 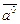 :
: 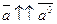 и
и 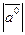 =1.
=1.
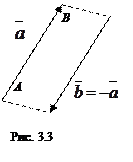 Вектор
Вектор  называется противоположным вектору
называется противоположным вектору  , если они противоположно направлены и их модули равны:
, если они противоположно направлены и их модули равны: 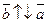 и
и 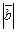 =
= 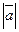 . Обозначается: -
. Обозначается: -  . Из рис. 3.3 ясно, что если
. Из рис. 3.3 ясно, что если 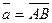 , то
, то 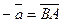 , т.к.
, т.к. 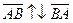 и
и 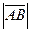 =
= 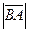 .
.
Дата добавления: 2015-07-20; просмотров: 80 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные задачи аналитической геометрии в пространстве. | | | Линейные операции над векторами. |