Свойства определителей.

Приведенные ниже свойства справедливы для определителей любого порядка.

Свойство 1. Определитель не изменится, если его строки заменить столбцами с теми же номерами, т. е.

, .

Эта операция называется транспонированием, т. е. при транспонировании определитель не меняется. Проверяется непосредственно.

Это свойство показывает равноправие строк и столбцов определителя.

Свойство 2. При перестановке двух строк (столбцов) определитель меняет знак.

Свойство 3. Определитель, имеющий две одинаковые строки (столбца), равен нулю.

Свойство 4. Общий множитель любой строки (столбца) можно вынести за знак определителя.

В частности, если определитель имеет нулевую строку (столбец), то он равен нулю.

Свойство 5. Если две строки (столбца) определителя пропорциональны, то определитель равен нулю.

Свойство 6. Если к элементам одной строки (столбца) определителя прибавить соответствующие элементы другой строки (столбца), умноженные на одно и то же число, то определитель не изменится:

.

Здесь к элементам первого столбца прибавлены элементы третьего столбца, умноженные на число k.

Это важное свойство легко проверить непосредственно.

Определение 3.Минором элемента определителя называется определитель 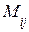, полученный из данного вычеркиванием строки и столбца, на пересечении которых стоит данный элемент.

Определение 4.Алгебраическимдополнением элемента определителя называется число . (1.2)

Пример. Найти если .

Итак, алгебраическое дополнение совпадает с минором элемента определителя , если – четное число, и отличается знаком, если – нечетное число. Для запоминания приведем "правило знаков": .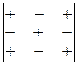

Свойство 7. Разложениеопределителяпостроке (столбцу). Определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения: . (1.3)

Заметим, что для определителя третьего порядка таких равенств можно написать шесть (по числу строк и столбцов).

Свойство 7 позволяет свести вычисление определителя данного порядка n к вычислению определителей более низших порядков, что особенно важно при вычислении определителей четвертого и более высоких порядков, даже определение которых достаточно громоздко.

Проверим формулу (1.3).

Пример. Вычислить определители:

1) , 2) .

Решение. 1) Вычислим , разложив его по первой строке:

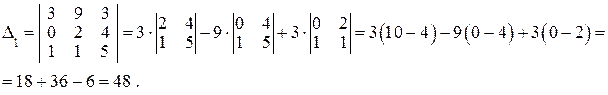
2) Вычислим 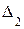, разложив его по третьему столбцу:

Заметим, что при вычислении определителя количество вычислений уменьшается, если данная строка (столбец) содержит нули.

Свойство 8. Сумма произведений элементов одной строки определителя на алгебраические дополнения соответствующих элементов другой строки равна нулю.

Дата добавления: 2015-07-20