
Читайте также:
|
Теорема 1. (О базисе на плоскости). Любые два нулевых неколлинеарных вектора 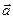 и
и 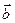 на плоскости образуют базис, т. е. любой третий вектор
на плоскости образуют базис, т. е. любой третий вектор 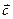 плоскости может быть единственным образом представлен как линейная комбинация векторов
плоскости может быть единственным образом представлен как линейная комбинация векторов 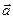 и
и 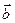 :
:
 (3.1)
(3.1)
Доказательство: Приложим все три вектора  ,
,  ,
, 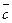 к одному началу 0. Построим параллелограмм, две стороны которого лежат на прямых, проходящих через векторы
к одному началу 0. Построим параллелограмм, две стороны которого лежат на прямых, проходящих через векторы  и
и 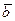 , а вектор
, а вектор 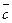 является диагональю этого параллелограмма (см. рис. 3.10):
является диагональю этого параллелограмма (см. рис. 3.10):
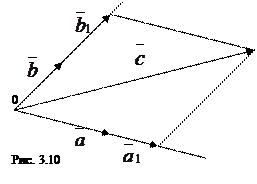 Тогда
Тогда 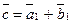 , где
, где  1||
1||  , поэтому
, поэтому  1=α
1=α  , а
, а  1||
1||  , поэтому
, поэтому  1=β
1=β  . Следовательно
. Следовательно 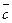 = α
= α  + β
+ β  .
.
Из приведенного доказательства ясно, что числа α и β определяются единственным образом.
Определение. Числа α и β в разложении (3.1) вектора 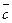 называются координатами вектора
называются координатами вектора 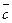 в базисе
в базисе  и
и  .
.
Определение. Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. В противном случае они называются некомпланарными.
Теорема 2. (О базисе в пространстве). Любые три нулевых вектора  ,
,  ,
, 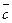 образуют базис в пространстве; т.е. любой четвертый вектор
образуют базис в пространстве; т.е. любой четвертый вектор 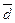 пространства может быть единственным образом представлен как линейная комбинация векторов
пространства может быть единственным образом представлен как линейная комбинация векторов  ,
,  ,
, 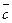 :
:
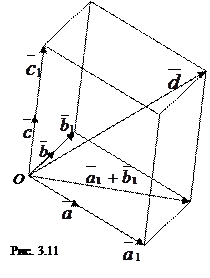
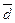 =α
=α  +β
+β  +γ
+γ 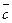 (3.2)
(3.2)
Доказательство: Приложим векторы  ,
,  ,
, 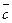 и
и 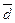 к одному началу 0. Проведем через конец вектора
к одному началу 0. Проведем через конец вектора 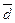 плоскости, параллельные плоскостям, определяемым парами векторов
плоскости, параллельные плоскостям, определяемым парами векторов 
 ,
, 
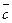 ,
, 
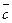 (см. рис. 3.11).
(см. рис. 3.11).
В возникшем параллелепипеде вектор 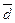 является диагональю, поэтому
является диагональю, поэтому 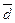 =
=  1+
1+  1+
1+ 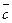 1=α
1=α  +β
+β  +γ
+γ 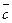 .
.
Из построений ясно, что числа α, β, γ, называемые координатами вектор 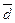 в базисе из векторов
в базисе из векторов  ,
,  ,
, 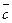 , определяются единственным образом.
, определяются единственным образом.
Заметим, что равенство (3.2) называется разложением вектора 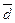 по базису из векторов
по базису из векторов  ,
,  ,
, 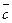 .
.
Равенство векторов в координатной форме: векторы равны тогда и только тогда, когда равны их соответствующие координаты в данном базисе.
Дата добавления: 2015-07-20; просмотров: 233 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Линейные операции над векторами. | | | Проекция вектора на ось. |