
Читайте также:
|
Скалярное произведение может быть вычислено по формуле
 .
.
Длина вектора – это скаляр, равный арифметическому квадратному корню из суммы квадратов координат (компонент) вектора.
Расстояние d между двумя точками 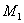 (
(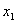 ,
,  ,
,  ) и
) и  (
(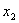 ,
,  ,
,  ) в пространстве определяется формулой
) в пространстве определяется формулой
 .
.
 Скалярным произведением двух векторов называется произведение длин двух векторов на косинус угла между ними.
Скалярным произведением двух векторов называется произведение длин двух векторов на косинус угла между ними.
Дата добавления: 2015-07-25; просмотров: 102 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Действие с геометрическими векторами в координатной форме. Признак коллениарности. | | | Уравнение прямой, Проходящей через две заданные точки на плоскости и в пространстве. |