|
Читайте также: |
Начнем с определения окружности, известного из школьного курса математики.
Определение 12.2 Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности.
Получим уравнение окружности, если известны ее центр и радиус.
Теорема 12.1 Окружность радиуса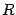 
с центром в точке 
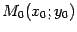имеет уравнение
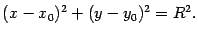
Доказательство. Пусть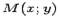 
-- текущая точка окружности. По определению окружности расстояние 
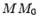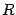равно (рис. 12.1)
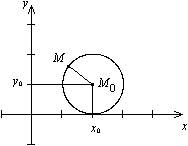
Рис.12.1.Окружность
По формуле (10.4) для плоскости получаем, что точки окружности и только они удовлетворяют уравнению
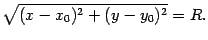
Обе части уравнения неотрицательны. Поэтому после возведения их в квадрат получим эквивалентное уравнение (12.2).
Если в уравнении (12.2) раскрыть скобки и привести подобные члены, то вид его изменится. Однако любое уравнение окружности с помощью тождественных преобразований можно привести к виду (12.2). Для этого достаточно выделить полные квадраты по переменным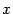 
и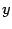 
Дата добавления: 2015-07-25; просмотров: 63 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Угол между прямой и плоскостью | | | Определения определителя и его свойства. |