Читайте также:
|
Угол между двумя плоскостями в пространстве j связан с углом между нормалями к этим плоскостям j1 соотношением: j = j1 или j = 1800 - j1, т.е.
cosj = ±cosj1.
Определим угол j1. Известно, что плоскости могут быть заданы соотношениями:
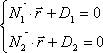
, где
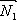(A1, B1, C1), 
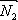(A2, B2, C2). Угол между векторами нормали найдем из их скалярного произведения:
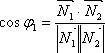
Таким образом, угол между плоскостями находится по формуле:
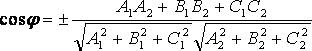
Выбор знака косинуса зависит от того, какой угол между плоскостями следует найти – острый, или смежный с ним тупой.
Дата добавления: 2015-07-25; просмотров: 64 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Уравнение прямой, Проходящей через две заданные точки на плоскости и в пространстве. | | | Условия параллельности и перпендикулярности плоскостей |