Читайте также:
|
Матрица A-1 называется обратной матрице А, если выполняется условие
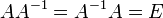
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.
Свойства обратной матрицы
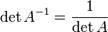, где det обозначает определитель.
(AB) − 1 = B − 1A − 1 для любых двух обратимых матриц A и B.
(AT) − 1 = (A − 1)T, где * T обозначает транспонированную матрицу.
(kA) − 1 = k − 1A − 1 для любого коэффициента k не ровно 0
Если необходимо решить систему линейных уравнений Ax = b, (b — ненулевой вектор) где x — искомый вектор, и если A - 1 существует, то x = A − 1b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
Дата добавления: 2015-07-25; просмотров: 64 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Определения определителя и его свойства. | | | Система линейных уравнений. Определение совместной, не совместной системы |