Окружность

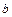
Окружность – множество всех точек плоскости,

удаленных от заданной точки А плоскости – центра

окружности – на одно и то же расстояние R – радиус

окружности.

В прямоугольной системе координат уравнение окружности (каноническое уравнение окружности):

(x – a)² + (y – b)² = R ²,

где (a, b) – координаты ее центра.

В частности, если a = 0, b = 0 (центр совпадает с началом координат), то уравнение окружности имеет вид:

x ² + y ² = R ².

Общее уравнение второй степени (1) определяет окружность, если А = С ≠ 0 и В = 0.

Пример 1. Найти координаты центра и радиус окружности:

а) х ² + у ² – 4 х + 8 у – 16 = 0; а) 9 х ² + 9 у ² + 42 х – 54 у – 95 = 0.

• а) Выделяем полные квадраты в левой части уравнения:

х ² + у ² – 4 х + 8 у – 16 = х ²– 4 х + 4 – 4 + у ² + 8 у + 16 – 16 – 16 = (х – 2) ² + (у + 4) ² = 6².

Центр окружности находится в точке О (2; -4), а радиус равен 6.

б) Разделив обе части уравнения на 9, найдем х ² + у ² + х – 6 у – = 0. Выделяем полные квадраты по х и по у в левой части уравнения:

х ² + х + + у ² – 6 у + 9 – – 9 – = (х + )² + (у –3) ² = 5².

Центр окружности находится в точке О (– ; 3), а радиус R = 5.

Пример 2. Написать уравнения касательных к окружности х ² + у ² – 6 х + 4 у – 12 = 0,

проведенных из точки М (0; 3).

• Уравнения касательных должны иметь вид (в виде уравнений прямых с угловым коэффициентом) y = kx + 3. Уравнение окружности приведем к каноническому виду, выделяя полные квадраты по х и по у:

х ² + у ² – 6 х + 4 у – 12 => (х – 3) ² + (у + 2) ² = 25.

Для нахождения общих точек прямой и окружности надо решить систему уравнений 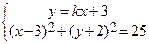. Имеем: (х – 3) ² + (kx + 3 + 2) ² = 25, т.е.

х ²– 6 х + 9 + k ² x ² + 10 kx + 25 = 25, поэтому (k ² + 1) x ² + (10 k – 6) x + 9 = 0. Т.к. прямая касается окружности, то это уравнение имеет единственное решение. Следовательно, его дискриминант равен нулю, т.е. (5 k – 3) ² – 9(k ² + 1) = 0, откуда k ₁ = 0, k ₂ = . Значит, у = 3 и у = х + 3 – искомые уравнения.

Пример 3. Написать уравнение окружности, проходящей через точки

(–1; 3), (0; 2), (1; –1).

• Уравнение окружности ищем в виде (х – a)² + (у – b) ² = R ². Подставляя в это уравнение координаты данных точек, получим три уравнения для определения

a, b и R: . Из первых двух уравнений получаем (–1 – a)² + (3– b) ² = a ² + (2– b) ², т.е. 1 + 2 a + a ² + 9 – 6 b + b ² = a ² + 4 – 4 b + b ², поэтому

a – b = – 3; из второго и третьего уравнений системы получаем

a ² + (2– b) ² = (1 – a)² + (–1– b)², отсюда a – 3 b = – 1. Решая систему уравнений , находим a = – 4, b = – 1. Подставляя эти значения a и b во второе уравнение первоначальной системы, находим: 16 + 9 = R ², т.е. R ² = 25.

Т.о., искомое уравнение есть (х + 4)² + (у +1)² = 25.

Эллипс

Эллипс – множество точек плоскости,

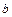
сумма расстояний от каждой из которых до

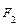
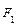
двух данных точек – фокусов эллипса –

величина постоянная, большая, чем

расстояние между фокусами.

Каноническое уравнение эллипса:

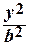+ = 1, (2)

а – большая полуось, b – малая полуось эллипса.

Координаты фокусов: F ₁(- c; 0), F ₂(c; 0), где с – половина расстояния между фокусами. Числа a, b и c связаны соотношением: с ² = а ² – b ².

Точки A, B, C, D – вершины эллипса, точка О – центр эллипса, расстояния r ₁ и r ₂ от произвольной точки М эллипса до его фокусов называются фокальными радиусами этой точки.

Эксцентриситетом эллипса называется отношение ε = (ε < 1, т.к. с < а).

Фокальные радиусы: r ₁ = а + εх, r ₂ = а – εх (r ₁ + r ₂ = 2 а).

Директрисами эллипса называются прямые l ₁ и l ₂ параллельные малой оси и отстоящие от нее на расстоянии, равном ; уравнения директрис: х = – 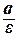, х = .

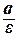Если а = b, то уравнение (2) определяет окружность x ² + y ² = а ².

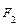
Если фокусы эллипса лежат на оси Оу, то эллипс имеет вид,

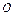
изображенный на рисунке. В этом случае:

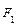
b > a, с ² = b ² – a ², ε = , уравнения директрис у = .

Уравнение эллипса с осями, параллельными

координатным:

+ = 1,

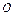где (х ₀; у ₀) – координаты центра эллипса.

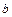
Параметрические уравнения эллипса:

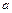
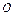
, t 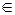[0; 2 π ].

t – угол между осью Ох и прямой ОМ, соединяющей

центр эллипса с его точкой М.

Пример 4. Показать, что уравнение 4 х ² + 3 у ² – 8 х + 12 у – 32 = 0 определяет эллипс,

найти его оси, координаты центра и эксцентриситет.

• Преобразуем данное уравнение кривой (выделяем полные квадраты по х и по у в левой части уравнения):

4 х ² + 3 у ² – 8 х + 12 у – 32 = 4(х ²– 2 х + 1 – 1) + 3(у ² + 4 у + 4 – 4) – 32 = 4(х – 1)² + 3(у + 2)² = 48,

т.е. + 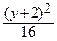= 1. Получили каноническое уравнение эллипса, центр симметрии которого имеет координаты (1; –2). Из уравнения находим: а ² = 12,

а = 2 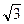и b ² = 16, b = 4 (b > a). Поэтому с = = = 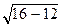2. Эксцентриситет эллипса ε = = .

Пример 5. Дано уравнение эллипса 24 х ² + 49 у ² = 1176. Найти

1) длины его полуосей;

2) координаты фокусов;

3) эксцентриситет эллипса;

4) уравнения директрис и расстояние между ними;

5) точки эллипса, расстояние от которых до левого фокуса F ₁ равно 12.

• Разделив правую и левую части уравнения на 1176, получим каноническое уравнение эллипса: + = 1.

1) Отсюда а ² = 49, b ² = 24, т.е. а = 7, b = 2 .

2) с = = = 5. Следовательно, F ₁ (–5; 0) и F ₂ (5; 0).

3) a > b = > ε = = .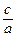

4) Уравнения директрис имеют вид: х = ± = ± = ± .

Расстояние между ними d = – = = 19,6.

5) По формуле r ₁ = a + ε x находим абсциссу точек, расстояние от которых до точки F ₁ равно 12: 12 = 7 + 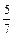х, т.е. х = 7. Подставляя значение х в уравнение эллипса, найдем ординаты этих точек: 24 · 49 + 49 у ² = 1176, 49 у ² = 0, у = 0.

Условию задачи удовлетворяет точка А (7; 0).

Пример 6. Составить уравнение эллипса, проходящего через точки А (2; – 4 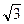) и

В (–1; 2 ).

• Уравнение эллипса ищем в виде 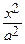+ 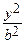= 1. Подставляя в это уравнение координаты данных точек, получим два уравнения для определения a и b: + 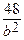= 1 и 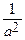+ = 1. Умножая второе уравнение на (–4) и складывая с первым, находим – = –3, т.е. b ² = 64. Подставляя полученное значения b ² в первое уравнение, получаем + = 1, откуда а ² = 16.

Т.о., искомое уравнение эллипса есть + = 1.

Пример 7. Найти уравнение касательной к эллипсу + = 1 перпендикулярно

прямой х – у + 50 = 0.

• Уравнение касательной должно иметь вид (в виде уравнения прямой с угловым коэффициентом) y = kx + с.

Угловой коэффициент k найдем из условия k · k ₁ = –1 перпендикулярности прямых, где k ₁ – угловой коэффициент прямой х – у + 50 = 0. Т.к. k ₁ = 1 (у = х + 50), то

k = –1, уравнение касательной к эллипсу имеет вид у = – х + с. Общие точки прямой и эллипса находим, решая систему уравнений .

Получаем + = 1, т.е. 5 х ² – 8 сх + 4 с ² – 20 = 0. Уравнение имеет единственное решение (прямая касается эллипса, т.е. имеет с ним единственную общую точку) лишь в случае, когда его дискриминант равен нулю, т.е.

64 с ² – 4 · 5(4 с ² – 20) = 0 или 4 с ² – 5(с ² – 5) = 0. Значит, есть два решения:

с ₁ = 5 и с ₂ = -5. Условию задачи удовлетворяют две касательные:

у = – х + 5 и у = – х – 5.

Пример 8. Составить уравнение эллипса, фокусы которого лежат на оси Оу, а малая

ось равна 2 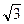. Каждый из фокусов равноудален от центра эллипса и от

ближайшего конца фокальной оси.

• Уравнение эллипса имеет вид 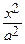+ 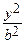= 1, b > a. По условию задачи 2 а =2 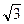, т.е. а = 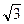, и с = . Т.к. с ² = b ² – a ², то получаем: = b ² – 3, т.е. b ² = 4. Т.о., уравнение эллипса есть + = 1.

Гипербола

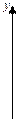Гиперболой называется множество точек

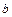
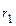плоскости, модуль разности расстояний от

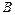
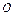
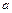
каждой из которых до двух заданных точек –

фокусов, есть величина постоянная, меньшая,

чем расстояние между фокусами.

Каноническое уравнение гиперболы:

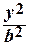– = 1, (3)

а – действительная полуось, b – мнимая полуось гиперболы.

Координаты фокусов: F ₁(- c; 0), F ₂(c; 0), где с – половина расстояния между фокусами. Числа a, b и c связаны соотношением: с ² = а ² + b ².

Точки A и B – вершины гиперболы, точка О – центр гиперболы, расстояния r ₁ и r ₂ от произвольной точки М гиперболы до его фокусов называются фокальными радиусами этой точки.

Эксцентриситет гиперболы: ε = (ε > 1, т.к. с > а).

Фокальные радиусы:

для правой ветви гиперболы: r ₁= а + εх, r ₂ = - а + εх (| r ₁ – r ₂| = 2 а),

для левой ветви гиперболы: r ₁= – а – εх, r ₂= а – εх (| r ₁ – r ₂| = 2 а),

Прямоугольник, центр которого совпадает с точкой О, а стороны равны соответственно 2 а и 2 b и параллельны осям гиперболы, называется прямоугольником гиперболы. Диагонали прямоугольника гиперболы лежат на двух прямых, называемых асимптотами гиперболы. Они определяются уравнениями:

у = х.

Директрисами гиперболы называются прямые l ₁ и l ₂ параллельные мнимой оси и отстоящие от нее на расстоянии, равном ; их уравнения:

х = – 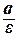, х = .

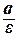Если а = b, то гипербола (3) называется равносторонней:

x ² – y ² = а ².

Если фокусы гиперболы лежат на оси Оу, то

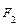
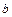
уравнение гиперболы имеет вид: – 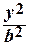= - 1. (4)

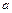
В этом случае: b > a, ε = , уравнения директрис

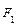
у = .

Гипербола (4) называется сопряженной гиперболе (3).

Уравнение гиперболы с осями, параллельными

координатным:

– = 1,

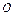
где (х ₀; у ₀) – координаты центра гиперболы.

Пример 9. Дано уравнение гиперболы 5 х ² – 4 у ² = 20. Найти

1) длины его полуосей;

2) координаты фокусов;

3) эксцентриситет гиперболы;

4) уравнения асимптот и директрис;

5) фокальные радиусы точки М (3; 2; 5).

• Разделив правую и левую части уравнения на 20, получим каноническое уравнение гиперболы: – = 1. Отсюда

1) а ² = 4, b ² = 5, т.е. а = 2, b = .

2) с = 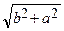= = 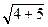3. Следовательно, F ₁ (–3; 0) и F ₂ (3; 0).

3) ε = = .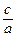

4) Уравнения асимптот и директрис имеют вид: у = ± х и х = ± = ± = ± .

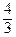5) Точка М лежит на правой ветви гиперболы (х = 3 > 0), следовательно,

r ₁ = 2 + · 3 = 6,5, r ₂ = –2 + · 3 = 2,5.

Пример 10. Составить уравнение гиперболы, если ее фокусы лежат на оси Оу и

расстояние между равно 10, а длина действительной оси равна 8.

• Уравнение гиперболы имеет вид 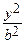– 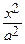= 1. По условию задачи 2 с =10, т.е

с = 5; 2 b = 8, b = 4.

Т.к. с ² = a ² + b ², то получаем: 25 = a ² + 16, т.е. a ² = 9, a = 3. Т.о., уравнение гиперболы – = 1.

Пример 11. Составить уравнение гиперболы, фокусы которой находятся в точках

F ₁ (-2; 4) и F ₂ (12; 4), а длина мнимой оси равна 6.

• Центр гиперболы лежит на прямой у = 4, параллельной оси Ох. Уравнение гиперболы имеет вид – 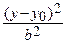= 1. По условию задачи 2 b =6, т.е b = 3. 2 b = 8, b = 4. Расстояние между фокусами равно 14, т.е. 2 с = 14, с = 7.

Т.к. с ² = a ² + b ², то: 49 = a ² + 9, т.е. a ² = 40, a = 2 . Центр гиперболы делит расстояние между фокусами пополам. Поэтому

х ₀ = 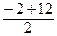= 5, у ₀ = = 4.

Т.о., уравнение гиперболы – = 1.

Пример 12. Найти угол между асимптотами гиперболы, если ее эксцентриситет

равен 2.

• Уравнения асимптот гиперболы: у = ± 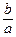х. Найдем отношение 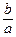: ε = 2,

ε = 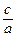= = . Отсюда 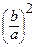= ε ² – 1, т.е. 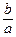= 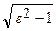. Имеем: 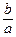= = 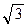. Т.о., уравнения асимптот гиперболы есть у = ± 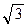х. Угол φ между асимптотами найдем по формуле tg 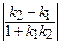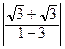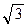φ = = = , φ = .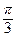

Пример 13. Дан эллипс 5 х ² + 8 у ² = 40. Найти уравнение гиперболы, вершины

которой находятся в фокусах, а фокусы – в вершинах данного эллипса.

Найдем координаты вершин А и В и фокусов эллипса, записав его

уравнение в канонической форме + = 1. Имеем а ² = 8,

а = 2 ; b ² = 5, а = .

Из соотношения с ² = a ²– b ² находим с: с ² = 8 – 5, с = 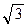. Можно записать:

А (2 ; 0), В (–2 ; 0), F ₁ (– 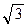; 0) и F ₂ (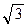; 0). Обозначим через а_g, b_g, c_g – соответственно полуоси гиперболы и половину расстояния между ее фокусами. Тогда, согласно условиям задачи, можно записать: а_g = OF ₂, т.е. а_g = 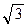и c_g = ОА, т.е. c_g = 2 . Из соотношения = + находим 8 = 3 + , поэтому =5, b_g = . Подставляя найденные значения этому шения м задачрболы и половину расстояния между ее фокусами. а_g и b_g в уравнение гиперболы, находим

– = 1 – искомое уравнение гиперболы.

Парабола

Параболой называется множество точек

плоскости, каждая из которых равноудалена от

заданной точки фокуса, и заданной прямой –

Дата добавления: 2015-07-25