Читайте также:
|
Под углом между плоскостями понимается угол между нормальными векторами этих плоскостей.
Если плоскости Q 1 и Q 2 заданы уравнениями
А 1 х + В 1 у + С 1 z + D 1 = 0 и А 2 х + В 2 у + С 2 z + D 2 = 0,
нормальные вектора которых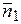 
= { A 1; B 1; С 1} и
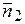= { A 2; B 2; С 2}, то:
cos φ =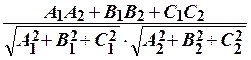 
.
Наименьший из двух смежных углов, образованных этими плоскостями, равен
cos φ =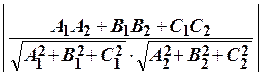 
.
Условие параллельности плоскостей Q 1 и Q 2: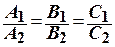 
.
Условие перпендикулярности плоскостей Q 1 и Q 2:
A 1 А 2 + B 1 B 2 + C 1 C 2 = 0.
Дата добавления: 2015-07-25; просмотров: 63 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Различные виды уравнения плоскости | | | Расстояние d от точки М0 до плоскости |