
Читайте также:
|
Каждая плоскость в пространстве Охуz определяется линейным
уравнением первой степени с тремя неизвестными.
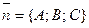



 Уравнение плоскости, проходящей через
Уравнение плоскости, проходящей через 


 точку М 0 (x 0; у 0; z 0) перпендикулярно
точку М 0 (x 0; у 0; z 0) перпендикулярно
вектору  = { A; B; С }:
= { A; B; С }:





 А (х - x 0) + В (y - y 0) + C (z - z 0) = 0.
А (х - x 0) + В (y - y 0) + C (z - z 0) = 0.
2. Уравнение пучка плоскостей, проходящих через прямую, образованную пересечением плоскостей А 1 х + В 1 у + С 1 z + D 1 = 0 и А 2 х + В 2 у + С 2 z + D 2 = 0 имеет вид:
А 1 х + В 1 у + С 1 z + D 1 + λ (А 2 х + В 2 у + С 2 z + D 2) = 0,
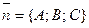

 где λ – числовой множитель.
где λ – числовой множитель.
 |
 Общее уравнение плоскости:
Общее уравнение плоскости:  |
 Ах + Ву + Сz + D = 0.
Ах + Ву + Сz + D = 0.
 |


 Вектор
Вектор  = { A; B; C } – нормальный вектор
= { A; B; C } – нормальный вектор
 плоскости (
плоскости ( перпендикулярен плоскости).
перпендикулярен плоскости).
Частные случая уравнения:
Ах + Ву + Cz = 0 (D = 0) – плоскость проходит через начало координат;
Ах + Ву + D = 0 (C = 0) – плоскость параллельна оси Оz (аналогичный смысл имеют уравнения Ах + Cz + D = 0 и Ву + Cz + D = 0);
Ах + Ву = 0 (D = C = 0 – плоскость проходит через ось Оz;
Ах + Cz = 0, Ву + Cz = 0 – через ось Оу и Ох соответственно);
Ах + D = 0 (В = С = 0 – плоскость параллельна плоскости Оуz;
Cz + D = 0, Ву + D = 0 – параллельна плоскости Оxу и Оxz соответственно);
Ах = 0, т.е. х = 0 (В = С = D = 0 – плоскость совпадает с плоскостью Оуz; y = 0, z = 0 – уравнения плоскостей Оxz и Оxy соответственно);




 Уравнение плоскости в отрезках:
Уравнение плоскости в отрезках:  = 1.
= 1.  |





 а, b, с – длины отрезков (с учетом знаков), отсекаемых
а, b, с – длины отрезков (с учетом знаков), отсекаемых
 плоскостью на осях Ох, Оу и Oz соответственно.
плоскостью на осях Ох, Оу и Oz соответственно.
















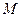







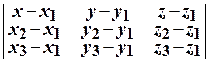 = 0.
= 0.
x cos α + y cos β + z cos γ – p = 0,
где р – длина перпендикуляра OK, опущенного из
начала координат на плоскость, α, β, γ – углы,
образованные этим перпендикуляром с положительными направлениями осей Ох, Оу и Oz соответственно
(cos2 α +cos2 β +cos2 γ = 1).
 Общее уравнение плоскости можно преобразовать в нормальное уравнение путем умножения на нормирующий множитель
Общее уравнение плоскости можно преобразовать в нормальное уравнение путем умножения на нормирующий множитель 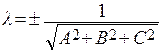 ; знак берется противоположным знаку свободного члена D (в общем уравнении плоскости).
; знак берется противоположным знаку свободного члена D (в общем уравнении плоскости).
Пример 13. Построить плоскости, заданные уравнениями:
а) 2 у – 5 = 0, б) х + z – 1 = 0, б) 3 х + 4 y + 6 z – 12 = 0.
• а) Плоскость 2 у – 5 = 0 параллельна плоскости Охz; она отсекает на оси Оу отрезок, равный 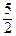 и имеет вид, изображенный на рис.а.
и имеет вид, изображенный на рис.а.
б) Плоскость х + z – 1 = 0 параллельна оси Оу; она пересекает плоскость Охz по прямой х + z = 1, отсекая на осях Ох и Оz отрезки, равные 1(рис.б).
в) Общее уравнение плоскости 3 х + 4 y + 6 z – 12 = 0 перепишем в виде
3 х + 4 y + 6 z = 12, т.е.  +
+ 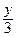 +
+  = 1 – уравнение плоскости в отрезках. Эта плоскость отсекает на осях Ох, Оу, Оz отрезки, равные 4, 3, 2 соответственно(рис.в).
= 1 – уравнение плоскости в отрезках. Эта плоскость отсекает на осях Ох, Оу, Оz отрезки, равные 4, 3, 2 соответственно(рис.в).
 | |||||
 | |||||
 | |||||
а б в
Пример 14. Уравнение плоскости 2 х – 6 y + 3 z – 14 = 0 привести к нормальному
виду.
• Умножим обе части уравнения на нормирующий множитель
λ =  =
= 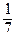 . Перед корнем стоит знак «+», т.к. свободный член С = –14 заданного уравнения отрицателен. Имеем:
. Перед корнем стоит знак «+», т.к. свободный член С = –14 заданного уравнения отрицателен. Имеем: 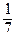 (2 х – 6 y + 3 z – 14)= 0, т.е.
(2 х – 6 y + 3 z – 14)= 0, т.е.
 х –
х –  y +
y +  z – 2= 0. Здесь р = 2, т.е. расстояние от точки О (0; 0; 0) до плоскости равно 2;cos α =
z – 2= 0. Здесь р = 2, т.е. расстояние от точки О (0; 0; 0) до плоскости равно 2;cos α =  ,cos β = –
,cos β = –  , cos γ =
, cos γ =  (cos2 α + cos2 β + cos2 γ =
(cos2 α + cos2 β + cos2 γ =  +
+  +
+  = 1).
= 1).
Пример 15. Написать уравнение плоскости:
а) параллельной оси Oz и проходящей через точки М 1 (3, –1, 2) и М 2 (–1, 2, 5);


 Подставляя найденные значения А и В в уравнение Ах + Ву + D =0, получаем
Подставляя найденные значения А и В в уравнение Ах + Ву + D =0, получаем  Dx
Dx  Dy + D =0. После сокращения на
Dy + D =0. После сокращения на  D получим 3 х + 4 у –5=0.
D получим 3 х + 4 у –5=0.
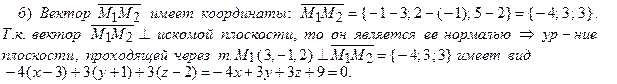

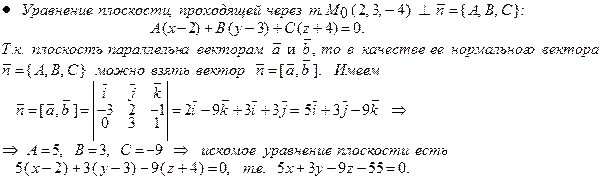

Пример 17. Написать уравнение плоскости, проходящей через три заданные
точки М 1 (1, 0, –1), М 2 (2, 2, 3), М 3 (0, –3, 1).
• Три точки, не лежащие на одной прямой, определяют в пространстве единственную плоскость. Ее уравнение будем искать в виде Ax + By + Cz + D = 0. Т.к. точки М 1, М 2 и М 3 лежат в одной плоскости, векторы  и
и  также лежат в ней (см. рис.). Векторное произведение [
также лежат в ней (см. рис.). Векторное произведение [  ,
,  ]
]

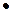






 перпендикулярно плоскости, в которой они лежат. Следовательно,
перпендикулярно плоскости, в которой они лежат. Следовательно,
в качестве нормального вектора 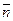 к плоскости можно взять вектор
к плоскости можно взять вектор
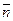 = [
= [  ,
,  ]. Координаты векторов
]. Координаты векторов  ,
,  и
и 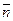 :
:
 = {2 – 1; 2 – 0; 3 – (–1)} = {1; 2; 4},
= {2 – 1; 2 – 0; 3 – (–1)} = {1; 2; 4},
 = {0 – 1; –3 – 0; 1 – (–1)} ={–1; –3; 2},
= {0 – 1; –3 – 0; 1 – (–1)} ={–1; –3; 2},
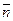 = [
= [  ,
,  ] =
] =  = 16
= 16 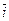 – 6
– 6 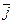 –
– 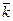 =>
=> 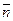 = {16, –6, –1}.
= {16, –6, –1}.
Т.о., параметры А, В и С плоскости равны 16, –6 и –1 соответственно и ожидаемый вид уравнения 16 x –6 y – z + D = 0. Для нахождения D подставим в это уравнение координаты любой из лежащих в ней точек М 1, М 2 или М 3 , например, М 1: 16 × 1–6 × 0– (–1) + D = 0=> D = –17.
Уравнение плоскости, проходящей через три заданные точки М 1 (1, 0, –1),
М 2 (2, 2, 3), М 3 (0, –3, 1) есть 16 x –6 y – z – 17 = 0.
Пример 18. Составить уравнение плоскости, проходящей через точку М (1, –2, 3)
и линию пересечения плоскостей 2 x – y + 2 z – 6 = 0 и 3 x + 2 y – z + 3 = 0.

Для нахождения второго решения положим х = 3 (подстановка z = 0 приводит к дробным решениям, что неудобно):  => М 3 (3, 8, –4). Далее, воспользовавшись способом, приведенным в примере 17, получим уравнение искомой плоскости 14 x + 7 y – 2 z + 6 = 0.
=> М 3 (3, 8, –4). Далее, воспользовавшись способом, приведенным в примере 17, получим уравнение искомой плоскости 14 x + 7 y – 2 z + 6 = 0.
Дата добавления: 2015-07-25; просмотров: 197 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, пересечение прямых | | | Угол между двумя плоскостями, условия параллельности и перпендикулярности двух плоскостей |