
Читайте также:
|
 ||
||  ó
ó  .
.
При сложении векторов их одноименные координаты складываются, при вычитании – вычитаются, при умножении вектора на число – умножаются на это число:

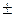
 = { ах
= { ах 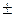 bх, аy
bх, аy 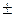 by, аz
by, аz 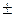 bz },
bz },
λ  = { λ ах, λ ау, λ аz }.
= { λ ах, λ ау, λ аz }.
Вектор  =
= 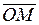 , соединяющий начало координат с произвольной точкой М (x, y, z)пространства называется радиус-вектором точки М. Координаты точки – это координаты ее радиус-вектора
, соединяющий начало координат с произвольной точкой М (x, y, z)пространства называется радиус-вектором точки М. Координаты точки – это координаты ее радиус-вектора  = { x, y, z } или
= { x, y, z } или  = x ∙
= x ∙  + y ∙
+ y ∙  + z ∙
+ z ∙  .
.
Если вектор  =
=  задан точками А (x 1, y 1, z 1) и В (x 2, y 2, z 2), то его координаты ах, ау, аz вычисляются по формулам
задан точками А (x 1, y 1, z 1) и В (x 2, y 2, z 2), то его координаты ах, ау, аz вычисляются по формулам
ах = x 2 – x 1, ay = y 2 – y 1, aх = z 2 – z 1:
 =
=  = { x 2 – x 1, y 2 – y 1, z 2 – z 1}.
= { x 2 – x 1, y 2 – y 1, z 2 – z 1}.
Пример 4. Даны точки А (3; –4; 1) и В (4; 6; –3). Найти координаты вектора  =
= 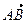 .
.
• Из координат конечной точки вычитаем координаты начальной точки. Имеем:
ах = 4 – 3 = 1, ay = 6 – (–4) = 10, аz = –3 – 1 = –4. Т.о.,  =
= 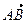 ={1; 10; –4}.
={1; 10; –4}.
Пример 5. Даны три последовательные вершины параллелограмма: А (1; –2; 3),
В (3; 2; 1), С (6; 4; 4). Найти координаты его четвертой вершины D.
• Обозначим координаты вершины D через х, у и z, т.е. D (х; у; z). Имеем:  =
= 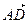 . Находим координаты векторов
. Находим координаты векторов  и
и 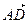 :
:
 ={6 – 3; 4 – 2; 4 – 1} = {3; 2; 3},
={6 – 3; 4 – 2; 4 – 1} = {3; 2; 3}, 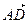 ={ x – 1; y + 2; z – 3}.
={ x – 1; y + 2; z – 3}.
Из равенства векторов  и
и 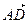 следует: x – 1 = 3, y + 2 = 2, z – 3 = 3. Отсюда:
следует: x – 1 = 3, y + 2 = 2, z – 3 = 3. Отсюда:
x = 4, y = 0, z = 6. Т.о., D (4; 0; 6).
Пример 6. Найти координаты вектора  , если известно, что он направлен в
, если известно, что он направлен в
противоположную сторону к вектору  = 5
= 5 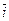 – 4
– 4 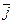 + 2
+ 2 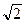
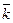 , и его модуль равен 5.
, и его модуль равен 5.
• Можно записать, что  = 5
= 5  . Т.к. вектор
. Т.к. вектор  направлен в противоположную сторону к вектору
направлен в противоположную сторону к вектору  , то
, то  = –
= –  . Найдем орт
. Найдем орт  . Из равенства
. Из равенства  = |
= |  | ×
| ×  находим
находим  =
=  . Но |
. Но |  | =
| = 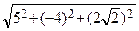 = 7. Значит,
= 7. Значит,  =
= 
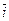 –
– 
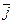 +
+ 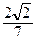
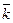 . Следовательно,
. Следовательно,  = –
= – 
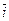 +
+ 
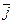 –
– 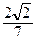
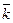 и
и  = 5
= 5  = –
= – 
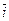 +
+ 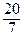
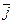 –
– 
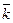 .
.
Пример 7. Вектор  составляет с осями Ох и Оу углы α = 60° и β = 120°. Найти
составляет с осями Ох и Оу углы α = 60° и β = 120°. Найти
его координаты, если |  | = 2.
| = 2.
• Пусть х, у, z – координаты вектора  , т.е.
, т.е.  = { x; y; z }. Координаты вектора
= { x; y; z }. Координаты вектора  найдем из соотношений cos α =
найдем из соотношений cos α =  , cos β =
, cos β =  , cos γ =
, cos γ = 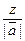 . Предварительно найдем cos γ из соотношения cos2 α + cos2 β + cos2 γ = 1: cos2 γ = 1 – cos2 α – cos2 β =
. Предварительно найдем cos γ из соотношения cos2 α + cos2 β + cos2 γ = 1: cos2 γ = 1 – cos2 α – cos2 β =
= 1 –  –
–  =
=  => cos γ = ±
=> cos γ = ± 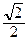 . Условию задачи удовлетворяют два вектора:
. Условию задачи удовлетворяют два вектора:  с направляющими косинусами cos α =
с направляющими косинусами cos α =  , cos β = –
, cos β = –  , cos γ =
, cos γ = 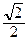 и
и  с направляющими косинусами cos α =
с направляющими косинусами cos α =  , cos β = –
, cos β = –  , cos γ = –
, cos γ = – 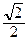 .
.
Т.к. направляющие косинусы – это координаты орта вектора  , то
, то
 = |
= |  | ×
| ×  = {2 ×
= {2 ×  ; 2 ×
; 2 ×  ; 2 ×
; 2 × 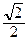 } = {1; –1;
} = {1; –1; 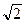 },
},
 = |
= |  | ×
| ×  = {2 ×
= {2 ×  ; 2 ×
; 2 ×  ; 2 ×
; 2 × 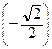 } = {1; –1; –
} = {1; –1; – 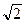 }
}
Пример 8. При каких значениях α и β векторы  = –2
= –2 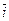 + 3
+ 3 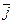 + α
+ α 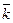 и
и
 = β
= β 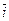 – 6
– 6 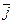 + 2
+ 2 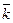 коллинеарны?
коллинеарны?
• Т.к.  ||
||  , то их координаты должны быть пропорциональными, т.е. должны выполняться равенства
, то их координаты должны быть пропорциональными, т.е. должны выполняться равенства  =
= 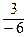 =
=  . Отсюда находим, что α = –1, β = 4.
. Отсюда находим, что α = –1, β = 4.
Пример 9. Разложить вектор 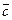 = {9; 4} по векторам
= {9; 4} по векторам  = {1; 2} и
= {1; 2} и  = {2; –3}.
= {2; –3}.
• Требуется представить вектор 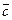 в виде линейной комбинации векторов.
в виде линейной комбинации векторов.  и
и  , т.е. в виде
, т.е. в виде 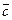 = λ
= λ  + m
+ m  , где λ и m – числа. Используя определение равенства векторов, получим {9; 4} = λ {1; 2} + m {2; –3} или
, где λ и m – числа. Используя определение равенства векторов, получим {9; 4} = λ {1; 2} + m {2; –3} или 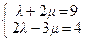 . Решая данную систему уравнений относительно λ и m, получим λ = 5, m = 2. Следовательно,
. Решая данную систему уравнений относительно λ и m, получим λ = 5, m = 2. Следовательно, 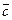 = 5
= 5  + 2
+ 2  .
.
Пример 10. Дана сила  = {4; 4; –4
= {4; 4; –4 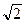 }. Найти величину и направление
}. Найти величину и направление  .
.
• Величина силы: |  | =
| =  = 8.
= 8.
Направляющие косинусы вектора  :
:
cos α =  =
=  =
=  , cos β =
, cos β =  =
=  =
=  , cos γ =
, cos γ = 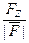 =
=  =
=  .
.
Т.о., сила  = 8 действует в направлении вектора, образующего с координатными осями углы α = 60°, β = 60°, γ = 135°.
= 8 действует в направлении вектора, образующего с координатными осями углы α = 60°, β = 60°, γ = 135°.
Дата добавления: 2015-07-25; просмотров: 120 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Обозначение:λ ∙ . | | | СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ |