
Читайте также:
|
 = { ах, ау, аz },
= { ах, ау, аz },  = { bх, bу, bz }, то (
= { bх, bу, bz }, то (  ,
,  ) = ах bх + ау bу + аz bz.
) = ах bх + ау bу + аz bz.
Пример 11. Векторы  и
и  образуют угол φ =
образуют угол φ = 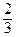 π. Зная, что |
π. Зная, что |  | = 10 и |
| = 10 и |  | = 2,
| = 2,
вычислить ( + 2
+ 2  , 3
, 3  –
–  ).
).
• Согласно свойствам скалярного произведения
( + 2
+ 2  , 3
, 3  –
–  ) = 3 (
) = 3 ( ,
,  ) – (
) – ( ,
,  ) + 6 (
) + 6 ( ,
,  ) – 2 (
) – 2 ( ,
,  ) = 3
) = 3  2 + 5 (
2 + 5 ( ,
,  ) – 2
) – 2  2 =
2 =
= 3 |  |2 + 5 |
|2 + 5 |  | × |
| × |  | × cos φ – 2 |
| × cos φ – 2 |  |2 = 3 × 100 + 5 × 10 × 2 ×
|2 = 3 × 100 + 5 × 10 × 2 ×  – 2 × 4 = 300 – 50 – 8 = 242.
– 2 × 4 = 300 – 50 – 8 = 242.
Пример 12. Дано: |  | = 2, |
| = 2, |  | = 1, φ = (
| = 1, φ = ( Ù
Ù  ) =
) = 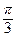 . Найти модуль вектора
. Найти модуль вектора
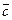 = 2
= 2  – 3
– 3  .
.
• Скалярный квадрат вектора 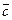 : |
: | 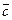 |2 =
|2 = 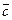 2 = (
2 = (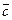 ,
, 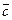 ) = (2
) = (2  – 3
– 3  , 2
, 2  – 3
– 3  ) =
) =
= 4 ( ,
,  ) – 6 (
) – 6 ( ,
,  ) – 6 (
) – 6 ( ,
,  ) + 9 (
) + 9 ( ,
,  ) = 4
) = 4  2 – 12 (
2 – 12 ( ,
,  ) + 9
) + 9  2 =
2 =
= 4 |  |2 – 12 |
|2 – 12 |  | × |
| × |  | × cos φ + 9 |
| × cos φ + 9 |  |2 = 4 × 4 – 12 × 2 × 1 ×
|2 = 4 × 4 – 12 × 2 × 1 ×  + 9 × 1 = = 16 – 12 + 9 = 13.
+ 9 × 1 = = 16 – 12 + 9 = 13.
Модуль вектора 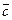 : |
: | 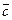 | =
| =  .
.
Пример 13. Найти вектор  , зная, что
, зная, что  ^
^  ,
,  = {1; 0; 1},
= {1; 0; 1},  ^
^  ,
,  = {0; 2; –1},
= {0; 2; –1},
проекция вектора  на вектор
на вектор 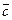 = {1; 2; 2} равна 1.
= {1; 2; 2} равна 1.
• Пусть вектор  имеет координаты
имеет координаты  = { x; y; z }.
= { x; y; z }.
1)  ^
^  => (
=> ( ,
,  ) = 0 => x + z = 0;
) = 0 => x + z = 0;
2)  ^
^  => (
=> ( ,
,  ) = 0 => 2 y – z = 0;
) = 0 => 2 y – z = 0;
3) prc  = 1 =>
= 1 =>  = 1 => || |
= 1 => || | 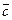 | =
| =  = 3|| => x + 2 y + 2 z = 3.
= 3|| => x + 2 y + 2 z = 3.
Получили систему уравнений  .
.
Решаем ее и находим: x = –  , y =
, y =  , z =
, z =  . Т.о.,
. Т.о.,  = –
= – 
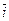 +
+ 
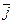 +
+ 
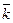 .
.
Пример 14. Даны вершины треугольника А (2; 3; –1), В (4; 1; –2), С (1; 0; 2). Найти:
а) внутренний угол при вершине С;
б)  .
.
• а) Угол φ при вершине С есть угол между векторами  и
и 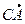 . Координаты этих векторов:
. Координаты этих векторов:
 = {4 – 1; 1 – 0; –2 – 2} = {3; 1; –4},
= {4 – 1; 1 – 0; –2 – 2} = {3; 1; –4}, 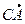 = {2 – 1; 3 – 0; –1 – 2} ={1; 3; –3}.
= {2 – 1; 3 – 0; –1 – 2} ={1; 3; –3}.
Модули этих векторов: |  | =
| =  =
=  , |
, | 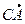 | =
| =  =
=  .
.
cos φ =  =
=  =
=  = > φ = arccos
= > φ = arccos  .
.
б)  =
=  =
=  .
.
Пример 15. Единичные векторы  ,
,  ,
,  удовлетворяют условию
удовлетворяют условию  +
+  +
+  =
=  .
.
Найти ( ,
,  ) + (
) + ( ,
,  ) + (
) + ( ×
×  ).
).
• Последовательно умножим скалярно равенство  +
+  +
+  =
=  на
на  ,
,  ,
,  :
:
( ,
,  ) + (
) + ( ,
,  ) + (
) + ( ×
×  ) = 0,
) = 0,
( ,
,  ) + (
) + ( ,
,  ) + (
) + ( ×
×  ) = 0,
) = 0,
( ,
,  ) + (
) + ( ,
,  ) + (
) + ( ×
×  ) = 0,
) = 0,
Сложим все три равенства. С учетом того, что ( ,
,  ) = (
) = ( ,
,  ) = (
) = ( ×
×  ) = 1, получим 2((
) = 1, получим 2(( ,
,  ) + (
) + ( ,
,  ) + (
) + ( ×
×  )) = –3. Следовательно,
)) = –3. Следовательно,
( ,
,  ) + (
) + ( ,
,  ) + (
) + ( ×
×  ) = –1,5.
) = –1,5.
Дата добавления: 2015-07-25; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ | | | ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ |