
|
Читайте также: |
Каждый вектор равен произведению его модуля на его орт:
 = |
= |  | ∙
| ∙ 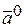 .
.
Признак коллинеарности векторов: два ненулевых вектора 
и  коллинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число:
коллинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число:  = λ
= λ  .
.
Признак компланарности векторов: три ненулевых вектора  ,
,  ,
,  компланарны тогда и только тогда, когда один из них является линейной комбинацией других, т.е.
компланарны тогда и только тогда, когда один из них является линейной комбинацией других, т.е.  = λ 1
= λ 1  + λ 2
+ λ 2  (λ 1 и λ 2 – одновременно не равные нулю числа).
(λ 1 и λ 2 – одновременно не равные нулю числа).
Пример 1. В треугольнике АВС дано: 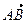 =
=  ,
, 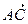 =
=  .
.






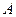
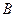
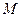






 Точка М – середина стороны ВС. Выразить вектор
Точка М – середина стороны ВС. Выразить вектор 
через векторы  и
и  .
.
• Через точку М проведем прямые, параллельные сторонам
АВ и АС. Получим параллелограмм АВ 1 МС 1 (см. рис.).
Следовательно,  =
=  +
+  . Т.к. В 1 М иС 1 М – средние
. Т.к. В 1 М иС 1 М – средние






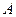
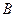



 линии, то АВ 1 = В 1 В, АС 1 = С 1 С и т.о.,
линии, то АВ 1 = В 1 В, АС 1 = С 1 С и т.о.,  =
= 
 +
+ 
 =
=  (
( +
+  ).
).
Пример 2. В параллелограмме АВСD дано: 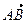 =
=  ,
, 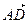 =
=  .
.
Выразить диагонали (векторы) 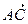 и
и  через
через  и
и  .
.
• См. рис.
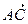 =
=  +
+  ,
,  =
=  –
–  .
.
Пример 3. Даны векторы  и
и  . Коллинеарны ли векторы
. Коллинеарны ли векторы 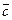 =
=  – 2
– 2 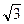
 и
и
 = –
= – 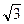
 + 6
+ 6  ?
?
•  = –
= – 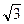
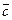 – выполняется условие коллинеарности векторов => векторы
– выполняется условие коллинеарности векторов => векторы  и
и  коллинеарны.
коллинеарны.



 Проекцией вектора
Проекцией вектора 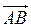 на
на  ось l называется
ось l называется
 число, равное
число, равное 



 длине вектора
длине вектора  , взятой со
, взятой со
 знаком «плюс», если направление вектора
знаком «плюс», если направление вектора 
совпадает с направлением оси и со знаком Рис.2.
«минус» в противном случае. Точки  и
и  –
–
проекции точек А и В на ось l (рис.2).
Обозначение: 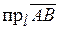 или
или  .
.
Основные свойства проекции:
1. 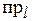 (
( +
+  ) =
) = 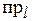
 +
+ 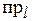
 ;
;
2. 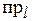 (λ
(λ  ) = λ ∙
) = λ ∙ 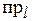
 ;
;
Если  ,
,  ,
,  – орты координатных осей прямоугольной системы координат Oxyz, то любой вектор
– орты координатных осей прямоугольной системы координат Oxyz, то любой вектор  единственным образом можно представить в виде их суммы (линейной комбинации) с коэффициентами ах, ау, аz:
единственным образом можно представить в виде их суммы (линейной комбинации) с коэффициентами ах, ау, аz:
 = ах ∙
= ах ∙  + аy ∙
+ аy ∙  + аz ∙
+ аz ∙  .
.
Коэффициенты ах, ау и аz линейной комбинации называются координатами вектора  в базисе
в базисе  ,
,  ,
,  .
.
Обозначение:  = { ах, ау, аz } или
= { ах, ау, аz } или  = ах ∙
= ах ∙  + аy ∙
+ аy ∙  + аz ∙
+ аz ∙  .
.
Координаты вектора  в базисе
в базисе  ,
,  ,
,  ,
,  = { ах, ау, аz }, совпадают с координатами точки М – конца вектора
= { ах, ау, аz }, совпадают с координатами точки М – конца вектора  =
= 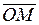 в прямоугольной системе координат Oxyz: М (ах, ау, аz).
в прямоугольной системе координат Oxyz: М (ах, ау, аz).
Длина вектора  определяется по формуле |
определяется по формуле |  | =
| =  .
.
Вектор  образует с координатными осями Ox, Oy и Oz углы α, β и γ соответственно.
образует с координатными осями Ox, Oy и Oz углы α, β и γ соответственно.
Направление вектора  определяется с помощью направляющих косинусов: cos α, cos β, cos γ, вычисляемых по формулам:
определяется с помощью направляющих косинусов: cos α, cos β, cos γ, вычисляемых по формулам:
cos α =  , cos β =
, cos β = 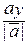 , cos γ =
, cos γ =  .
.
Направляющие косинусы связаны соотношением
cos2 α + cos2 β + cos2 γ = 1.
Координаты орта вектора  – это его направляющие косинусы:
– это его направляющие косинусы: 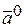 =
=  .
.
Пусть векторы 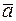 и
и 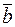 заданы своими координатами:
заданы своими координатами:
 = { ах, ау, аz } и
= { ах, ау, аz } и  = { bх, bу, bz }.
= { bх, bу, bz }.
Векторы  и
и  равны тогда и только тогда, когда равны их соответствующие координаты, т.е.
равны тогда и только тогда, когда равны их соответствующие координаты, т.е.  =
= 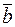 ó
ó  .
.
Дата добавления: 2015-07-25; просмотров: 57 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ. РАЗЛОЖЕНИЕ ВЕКТОРОВ | | | Векторы и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е. |