
Читайте также:
|
 = { ах, ау, аz },
= { ах, ау, аz },  = { bх, bу, bz },
= { bх, bу, bz },  = { cх, cу, cz }, то
= { cх, cу, cz }, то
(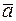 ,
, 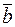 ,
, 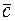 ) =
) = 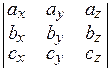 .
.
Если ( ,
,  ,
,  ) > 0, то
) > 0, то 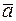 ,
, 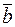 ,
, 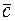 – правая тройка; (
– правая тройка; ( ,
,  ,
,  ) < 0 – левая.
) < 0 – левая.
Объем параллелепипеда, построенного на векторах 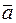 ,
,  и
и  :
:
V 1 = | ( ,
,  ,
,  )|.
)|.
Объем пирамиды, построенной на векторах 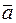 ,
,  и
и  :
:
V 2 = 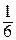 | (
| ( ,
,  ,
,  )|.
)|.
Пример 19. Доказать, что четыре точки А (3; 5; 1), В (2; 4; 7), С (1; 5; 3), D (4; 4; 5)
лежат в одной плоскости.
• Достаточно доказать, что три вектора 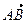 ,
, 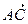 и
и 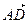 , имеющие начало в одной из данных точек, лежат в одной плоскости (т.е. компланарны). Координаты этих векторов:
, имеющие начало в одной из данных точек, лежат в одной плоскости (т.е. компланарны). Координаты этих векторов:
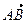 = {2 – 3; 4 – 5; 7 – 1} = {–1; –1; 6},
= {2 – 3; 4 – 5; 7 – 1} = {–1; –1; 6},
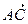 = {1 – 3; 5 – 5; 3 – 1} ={–2; 0; 2},
= {1 – 3; 5 – 5; 3 – 1} ={–2; 0; 2},
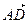 = {4 – 3; 4 – 5; 5 – 1} = {1; –1; 4}.
= {4 – 3; 4 – 5; 5 – 1} = {1; –1; 4}.
Проверяем условие компланарности векторов:
(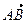 ,
, 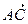 ,
, 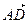 ) =
) = 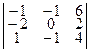 = 0 – 2 + 12 – 0 – 2 – 8 = 0 =>
= 0 – 2 + 12 – 0 – 2 – 8 = 0 =>
=> векторы 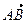 ,
, 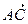 и
и 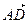 компланарны, следовательно, точки А, В, С, D лежат в одной плоскости.
компланарны, следовательно, точки А, В, С, D лежат в одной плоскости.
Пример 20. Даны вершины пирамиды А (5; 1; –4), В (1; 2; –1), С (3; 3; –4),
S (2; 2; 2). Найти длину высоты, опущенной из вершины S на грань АВС.
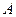
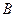
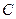





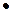
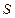
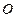
 • Т.к. объем V пирамиды равен V =
• Т.к. объем V пирамиды равен V = 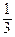 S осн h, то h =
S осн h, то h = 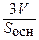 ,
,
где h – высота пирамиды, S осн – площадь основания.
Имеем: 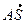 = {2 – 5; 2 – 1; 2 + 4} = {–3; 1; 6},
= {2 – 5; 2 – 1; 2 + 4} = {–3; 1; 6},
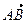 = {1 – 5; 2 – 1; –1 + 4} ={–4; 1; 3},
= {1 – 5; 2 – 1; –1 + 4} ={–4; 1; 3},
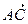 = {3 – 5; 3 – 1; –4 + 4} = {–2; 2; 0}.
= {3 – 5; 3 – 1; –4 + 4} = {–2; 2; 0}.
V = 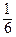
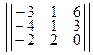 =
= 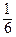 | 0 – 6 – 48 + 12 + 18 + 0 | =
| 0 – 6 – 48 + 12 + 18 + 0 | = 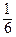 | –24 | = 4.
| –24 | = 4.
S осн =  | [
| [ 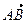 ,
, 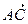 ] | =
] | = 
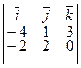 =
=  | –6
| –6 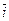 – 6
– 6 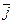 – 6
– 6 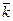 | =
| = 
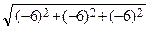 = 3
= 3 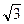 . Следовательно, h =
. Следовательно, h = 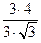 =
= 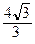 .
.
Пример 21. Вычислить ( +
+  +
+  ,
,  –
–  –
–  ,
,  –
–  +
+  ).
).
• Согласно свойствам смешанного произведения
( +
+  +
+  ,
,  –
–  –
–  ,
,  –
–  +
+  ) = ([
) = ([  +
+  +
+  ,
,  –
–  –
–  ],
],  –
–  +
+  ) = ([
) = ([  ,
,  ] – [
] – [  ,
,  ] – [
] – [  ,
,  ] +
] +
+ [  ,
,  ] – [
] – [  ,
,  ] – [
] – [  ,
,  ] + [
] + [  ,
,  ] – [
] – [  ,
,  ] – [
] – [  ,
,  ],
],  –
–  +
+  ) = (0 – [
) = (0 – [  ,
,  ] – [
] – [  ,
,  ] –
] –
– [  ,
,  ] – 0 – [
] – 0 – [  ,
,  ] – [
] – [  ,
,  ] + [
] + [  ,
,  ] – 0,
] – 0,  –
–  +
+  ) = (–2[
) = (–2[  ,
,  ] – 2[
] – 2[  ,
,  ],
],  –
–  +
+  ) =
) =
= –2(([  ,
,  ] + [
] + [  ,
,  ]),
]),  –
–  +
+  ) = –2 ((
) = –2 (( ,
,  ,
,  ) – (
) – ( ,
,  ,
,  ) + (
) + ( ,
,  ,
,  ) – (
) – ( ,
,  ,
,  ) – (
) – ( ,
,  ,
,  ) + (
) + ( ,
,  ,
,  )) = –2 (0 – 0 + (
)) = –2 (0 – 0 + ( ,
,  ,
,  ) – 0 + (
) – 0 + ( ,
,  ,
,  ) + 0) = –2 × 2(
) + 0) = –2 × 2( ,
,  ,
,  ) = –4(
) = –4( ,
,  ,
,  ).
).
Дата добавления: 2015-07-25; просмотров: 66 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ | | | АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ |