Читайте также:
|
Каждая прямая на плоскости Оху определяется линейным
уравнением первой степени с двумя неизвестными. Обратно, каждое линейное уравнение ервого порядка с двумя неизвестными определяет некоторую прямую на плоскости.
1. 
Уравнение прямой с угловым коэффициентом:
y = kx + b.
 |
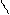Здесь: k – угловой коэффициент прямой (тангенс угла α,
который прямая образует с положительным направлением
оси Ох, k = tg α), b – ордината точки пересечения прямой с осью Оу.
|
2. 
Общее уравнение прямой:
Ах + Ву + С = 0.
Вектор 
= { A; B } – нормальный вектор прямой
( перпендикулярен прямой).
Частные случая уравнения:
Ах + Ву = 0 (С = 0) – прямая проходит через начало координат;
Ах + С = 0 (В = 0) – прямая параллельна оси Оу;
Ву + С = 0 (А = 0) – прямая параллельна оси Ох;
Ах = 0 (В = С = 0) – прямая совпадает с осью Оу;
Ву = 0 (А = С = 0) – прямая совпадает с осью Ох.
|
3. 
Уравнение прямой в отрезках: 
= 1.
а и b – длины отрезков (с учетом знаков), отсекаемых прямой на осях Ох и Оу соответственно.
Дата добавления: 2015-07-25; просмотров: 69 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ | | | Уравнение прямой, проходящей через данную точку в |