Читайте также:
|
СПРАВОЧНЫЕ МАТЕРИАЛЫ
ВЕКТОРНАЯ АЛГЕБРА
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ ВЕКТОРНАЯ АЛГЕБРА
ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ. РАЗЛОЖЕНИЕ ВЕКТОРОВ
Вектор – направленный отрезок. Вектор с началом в точке А и концом в точке В обозначается символом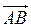 
(или одной буквой: 
, 
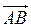, …, или: a, b, …). Длина отрезка АВ называется длиной (модулем) вектора и обозначается | 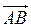|, | |, | a |.
Вектор, длина которого равна нулю, называется нулевым
вектором и обозначается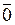 
(0).
Вектор, длина которого равна единице, называется единичным
вектором и обозначается через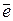 
(е).
Единичный вектор, направление которого совпадает с
направлением вектора , называется ортом вектора и обозначается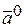 
.
Два вектора, имеющие одинаковую длину и противоположные
направления, называются противоположными. Вектор, противоположный вектору , обозначается – .
Векторы и называются коллинеарными, если они лежат на
одной прямой или на параллельных прямых. Записывают: || .
Три (и более) вектора называются компланарными, если они
лежат в одной плоскости или в параллельных плоскостях.
Два коллинеарных вектора и называются равными ( = ),
если они одинаково направлены и имеют равные длины.
Суммой двух векторов и называется вектор 
, соединяющий
начало вектора с концом вектора , отложенного от конца вектора . Обозначение: = + .
Геометрически сумма векторов получается с помощью правил
«треугольника» (рис.1а) или «параллелограмма» (рис.1.б):
а) б)
Рис.1.
Под разностью векторов и понимается вектор такой, что
+ = .
Обозначение: = – .
Справедливо равенство: – = + (– ).
Произведением вектора ≠ 
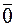на число
λ ≠ 0 называется вектор, имеющий длину | λ | ∙ | | и направление,
совпадающее с направлением вектора , если λ > 0; противоположное ему, если λ < 0.
Дата добавления: 2015-07-25; просмотров: 72 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Баку, 02 сентября 2002 г. 15 страница | | | Обозначение:λ ∙ . |