
|
Читайте также: |
 |
Векторным произведением вектора  на
на
вектор  называется вектор
называется вектор  , (рис.4) который
, (рис.4) который
1) перпендикулярен векторам  и
и  , т.е.
, т.е.


 и
и 

 (перпендикулярен плоскости, в
(перпендикулярен плоскости, в
которой лежат вектора  и
и  ); Рис.4.
); Рис.4.
2) имеет длину, численно равную площади параллелограмма,
построенного на векторах  и
и  как на сторонах, т.е. |
как на сторонах, т.е. |  | = |
| = |  | ∙ |
| ∙ |  | ∙ sin φ, где φ =
| ∙ sin φ, где φ =  ;
;
3) векторы  ,
,  и
и  образуют правую тройку. Три
образуют правую тройку. Три
некомпланарных вектора  ,
,  и
и  , взятые в указанном порядке, образуют правую (левую) тройку, если с конца вектора
, взятые в указанном порядке, образуют правую (левую) тройку, если с конца вектора  кратчайший поворот от первого вектора
кратчайший поворот от первого вектора  ко второму вектору
ко второму вектору  виден совершающимся против часовой стрелки (соотв. по часовой стрелке).
виден совершающимся против часовой стрелки (соотв. по часовой стрелке).
Обозначение: [  ,
,  ] или
] или  х
х  .
.
Векторное произведение можно выразить формулой [  ,
,  ] = S ∙
] = S ∙ 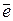 , где
, где 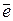 - орт направления [
- орт направления [  ,
,  ].
].
Свойства векторного произведения:
1. [  ,
,  ] = – [
] = – [ 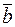 ,
,  ].
].
2. [  , (
, (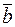 +
+  )] = [
)] = [  ,
, 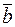 ] + [
] + [  ,
,  ].
].
3. [ λ  ,
, 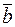 ] = [
] = [  , λ
, λ 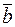 ] = λ [
] = λ [  ,
, 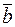 ].
].
4. Векторное произведение векторов равно нулю тогда и только тогда, когда sin φ = 0 (φ = 0) (перемножаемые векторы коллинеарны):
[  ,
,  ] =
] = 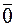 ó
ó  ||
||  (или
(или  =
= 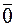 , или
, или  =
= 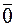 ).
).
В частности: [ 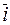 ,
, 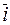 ] = [
] = [  ,
,  ] = [
] = [  ,
,  ] =
] = 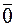 .
.
Если векторы  и
и  заданы своими координатами
заданы своими координатами
 = { ах, ау, аz },
= { ах, ау, аz },  = { bх, bу, bz }, то
= { bх, bу, bz }, то
[  ,
,  ] =
] =  или
или
[  ,
,  ] =
] =  .
.
Площадь параллелограмма, построенного на векторах  и
и  :
:
S = | [  ,
,  ]|.
]|.
Площадь треугольника, построенного на векторах  и
и  :
:
S Δ =  | [
| [  ,
,  ] |.
] |.
Момент силы относительно точки: пусть в точке А приложена сила  =
= 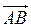 . Момент силы
. Момент силы  относительно точки О (рис.5) – это вектор
относительно точки О (рис.5) – это вектор  = [
= [  ,
,  ].
].
Линейная скорость вращения: скорость  точки М твердого тела, вращающегося с угловой скоростью
точки М твердого тела, вращающегося с угловой скоростью 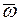 вокруг неподвижной оси, определяется формулой Эйлера:
вокруг неподвижной оси, определяется формулой Эйлера:  = [
= [ 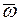 ,
,  ],
],
где  – радиус-вектор точки М (рис.6).
– радиус-вектор точки М (рис.6).

Рис.5. Рис.6.
Пример 16. Векторы  и
и  образуют угол φ =
образуют угол φ =  π. Зная, что |
π. Зная, что |  | = 2 и |
| = 2 и |  | = 6,
| = 6,
вычислить: а) | [  ,
,  ] |, б) | [2
] |, б) | [2  + 3
+ 3  ,
,  – 4
– 4  ] |.
] |.
• a) | [  ,
,  ] | = |
] | = |  | × |
| × |  | × sin φ = 2 × 6 ×
| × sin φ = 2 × 6 ×  = 6 ×
= 6 ×
б) [2  + 3
+ 3  ,
,  – 4
– 4  ] = 2 [
] = 2 [  ,
,  ] – 8[
] – 8[  ,
,  ] + 3 [
] + 3 [  ,
,  ] – 12 [
] – 12 [  ,
,  ] = || [
] = || [  ,
,  ] = [
] = [  ,
,  ] =
] =  || = 3
|| = 3  2 + 5 (
2 + 5 ( ,
,  ) – 2
) – 2  2 = – 8[
2 = – 8[  ,
,  ] – 3[
] – 3[  ,
,  ] = – 11[
] = – 11[  ,
,  ].
].
Следовательно, | [2  + 3
+ 3  ,
,  – 4
– 4  ] | = | –11[
] | = | –11[  ,
,  ] | = 11 × | [
] | = 11 × | [  ,
,  ] | = || см. а) || = 11 × 6 = 66.
] | = || см. а) || = 11 × 6 = 66.
Пример 17. Найти площадь треугольника с вершинами А (1; 2; 0), В (3; 2; 1),
С (–2, 1; 2).
• Площадь S треугольника АВС равна половине площади параллелограмма, построенного на векторах 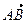 и
и 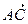 , т.е.S =
, т.е.S =  | [
| [ 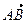 ,
, 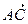 ] |.
] |. 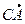 . Координаты этих векторов:
. Координаты этих векторов: 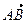 = {3 – 1; 2 – 2; 1 – 0} = {2; 0; 1},
= {3 – 1; 2 – 2; 1 – 0} = {2; 0; 1}, 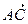 = {–2 – 1; 1 – 2; 2 – 0} ={–3; –1; 2}. Тогда [
= {–2 – 1; 1 – 2; 2 – 0} ={–3; –1; 2}. Тогда [ 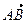 ,
, 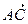 ] =
] =  =
= 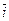 – 7
– 7 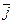 – 2
– 2 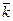 =>
=>
=> | [ 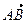 ,
, 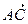 ] |=
] |=  = 3
= 3 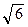 => S =
=> S =  .
.
Пример 18. Сила  = {2; –4; 5} приложена к точке А (0; 2; 1). Определить момент этой силы относительно точки О (–1; 2; 3).
= {2; –4; 5} приложена к точке А (0; 2; 1). Определить момент этой силы относительно точки О (–1; 2; 3).
• Момент силы  относительно точки О есть вектор
относительно точки О есть вектор 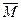 =[
=[  ,
,  ]. Координаты вектора
]. Координаты вектора  :
:  = {–1; 0; 2} =>
= {–1; 0; 2} =>
=> 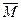 =[
=[  ,
,  ] =
] =  = 8
= 8 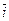 + 9
+ 9 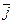 + 4
+ 4 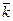 =>
=> 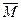 = {8; 9; 4}.
= {8; 9; 4}.
Дата добавления: 2015-07-25; просмотров: 109 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Если векторы и заданы своими координатами | | | СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ |