Угол между двумя прямыми, условия параллельности и перпендикулярности двух прямых, пересечение прямых

Под углом между прямыми l ₁ и l ₂ плоскости

понимается наименьший (острый) из двух смежных

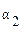
углов, образованных этими прямыми.

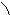
Если прямые заданы уравнениями с угловым

коэффициентом y = k ₁ x + b ₁и y = k ₂ x + b ₂,

то угол φ между ними равен: tg φ = .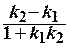

Условие параллельности прямых l ₁ и l ₂: k ₁ = k ₂.

Условие перпендикулярности прямых l ₁ и l ₂: k ₁ = – (или k ₁ k ₂ = – 1).

Если прямые l ₁ и l ₂ заданы общими уравнениями

А ₁ х + В ₁ у + С ₁ = 0 и А ₂ х + В ₂ у + С ₂ = 0,

то угол φ между ними равен углу между их нормальными векторами 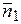= { A ₁; B ₁} и 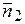= { A ₂; B ₂}:

cos φ = = или tg φ = .

Условие параллельности прямых l ₁ и l ₂:

(или A ₁ B ₂ – А ₂ B ₁ = 0).

Условие перпендикулярности прямых l ₁ и l ₂: A ₁ А ₂ + B ₁ B ₂ = 0.

Для нахождения общих точек прямых l ₁ и l ₂ необходимо решить систему уравнений

или

При этом:

если , то имеется единственная точка пересечения прямых;

если 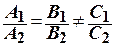, прямые не имеют общей точки, т.е. параллельны;

если 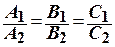, прямые совпадают.

Пример 8. Найти угол между прямыми:

а) у = 2 х – 3 и у = х + 5; б) 2 х – 3 у + 10 = 0 и 5 х – у + 4 = 0; в) у = 5 х + 1 и у = 5 х – 2.

• а) k ₁ = 2, k ₂ = => tg φ = = => φ = arctg (φ»37°);

б) = {2, –3}, = {5, –1} => (, ) = 2 × 5 + (–3) × (–1) = 13,

| | = = , | | = =

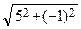cos φ = = = 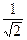=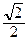> φ = ;

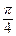в) k ₁ = 5, k ₂ = 5 => tg φ = 0 => φ = 0.

Пример 9. Исследовать взаимное расположение следующих пар прямых:

а) 3 х + 5 у – 9 = 0 и 10 х – 6 у + 4 = 0; б) 2 х + 5 у – 2 = 0 и х + у + 4 = 0;

в) 2 у = х – 1 и 4 y – 2 x + 2 = 0; г) х + 8 = 0 и 2 х – 3 = 0.

• а) А ₁ = 3, В ₁ = 5, С ₁ = –9; А ₂ = 10, В ₂ = –6, С ₂ = 4 => А ₁ × А ₂ + В ₁ × В ₂ =

= 3 × 10 + 5 × (–6) = 0 => прямые перпендикулярны;

б) А ₁ = 2, В ₁ = 5, С ₁ = –2; А ₂ = 1, В ₂ = 1, С ₂ = 4 => = , = =>

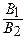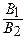=> ≠ => прямые не параллельны.

А ₁ × А ₂ + В ₁ × В ₂ = 2 × 1 + 5 × 1 = 7 ≠ 0 => прямые не перпендикулярны.

Следовательно, прямые пересекаются.

в) А ₁ = 1, В ₁ = –2, С ₁ = –1; А ₂ = –2, В ₂ = 4, С ₂ = 2 => = , = ,

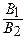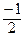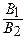= => = = => прямые совпадают.

г) х + 8 = 0 ó х = –8, 2 х – 3 = 0 ó х = => прямые параллельны.

Пример 10. Через точку пересечения прямых 3 х – 2 у + 5 = 0, х + 2 у – 9 = 0

проведена прямая, параллельная прямой 2 х + у + 6 = 0. Составить ее уравнение.

• Найдем точку М пересечения данных прямых. Для этого решим систему уравнений , из которой получаем х = 1, у = 4, т.е. М (1; 4).

Уравнение искомой прямой должно иметь вид 2 х + у + С = 0. Для нахождения С подставим в данное уравнение координаты точки М:2 × 1 + 4 + С = 0 => С = –6.

Т.о., уравнение искомой прямой 2 х + у – 6 = 0.

Пример 11. Найти координаты точки М ₂, симметричной точке М ₁(–3; 4)

относительно прямой 4 х – у – 1 = 0.

• Точки М ₁ и М ₂ лежат на перпендикуляре к заданной прямой. Уравнение этого перпендикуляра y = k ₁ x + b, где k ₁ = – , k = 4 – угловой коэффициент заданной прямой: k ₁ = – . Для нахождения b подставим в уравнение перпендикуляра координаты точки М ₁:4 = – × (–3) + b => b = . Следовательно, уравнение перпендикуляра y = – x + или х + 4 у – 13 = 0.

Найдем координаты точки М пересечения данных прямых. Для этого решим систему уравнений , из которой получаем х = 1, у = 3, т.е. М (1; 3).

Точка М делит отрезок М ₁ М ₂ пополам. Из соотношений 1 = и 3 = находим координаты х и у искомой точки М ₂: х = 5, у = 2, т.е. М ₂ (5; 2).

Дата добавления: 2015-07-25