Читайте также:
|
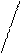
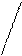
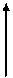
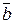
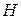
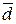Смешанным произведением трех векторов 
, 
и 
называется число, равное скалярному произведению вектора [ , ] на вектор (рис.7).
Рис.7.
Обозначение: (, , ) или .
Т.о.: (, , ) = ([ , ], ).
Геометрически смешанное произведение интерпретируется как число, равное объему параллелепипеда, построенного на векторах , и как на сторонах. Смешанное произведение векторов , и положительно, если эти векторы образуют правую тройку, и отрицательно – если левую.
Свойства смешанного произведения:
1. (, , ) = (, , ) =(, , ) – смешанное произведение не меняется при циклической перестановке векторов.
2. (, [ , ]) = ([ , ], ) – смешанное произведение не меняется при перестановке знаков векторного и скалярного умножения.
. 3. (, , 
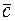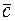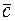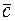) = – (, , ) = – (, , ) = – (, , ) – смешанное произведение меняет знак на противоположный при перемене мест любых двух векторов-сомножителей.
. 4. (, , ) = 0ó , и компланарны (в частности, если любые два из перемножаемых вектора коллинеарны).
Дата добавления: 2015-07-25; просмотров: 53 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ | | | Если векторы , и заданы своими координатами |