Читайте также:
|
Скалярным произведением двух ненулевых векторов 
и 
(рис.3) называется число, равное произведению длин этих векторов на косинус угла φ между ними:
( 
, 
) = | |∙| |∙ cos φ. (1)
Обозначение: (, ) или ∙ .
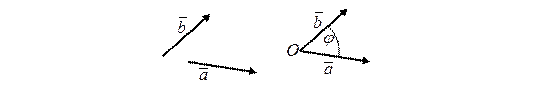
Рис.3.
Формулу (1) можно записать в виде:
( , ) = | 
|∙ пр 
или | | ∙ пр 
. (2)
Из формул (2) имеем: пр = 
, пр = 
.
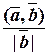Свойства скалярного произведения:
1. (, ) = (, ).
2. (, ( + 
)) = (, ) + (, ).
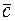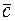3. ((λ ), ) = λ (, ).
4. 
= | | – скалярный квадрат вектора равен квадрату его модуля.
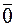5. Скалярное произведение векторов равно нулю тогда и только тогда, когда cos φ = 0 (φ = π /2) (перемножаемые векторы перпендикулярны): (, ) = 0 ó ┴ (или = 
, или
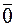= ). В частности: (
, 
) = (, 
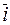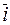) = (, ) = 0.
Дата добавления: 2015-07-25; просмотров: 71 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Векторы и коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е. | | | Если векторы и заданы своими координатами |