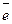
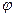
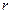
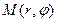
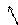
Полярная система координат

Полярная система координат задается

точкой О, называемой полюсом, лучом Ор,

называемым полярной осью, и единичным

вектором ē того же направления, что и луч Ор.

Положение точки М на плоскости определяется

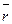
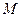
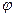
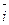
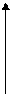двумя числами: ее расстоянием r от полюса О и

углом φ, образованном отрезком ОМ с полярной осью

и отсчитываемым в положительном направлении.

Числа r и φ называются полярными координа-

тами точки М: r называют полярным радиусом,

φ – полярным углом (0 ≤ r ≤ +∞, 0 ≤ φ ≤ 2 π).

Связь между полярными и прямоугольными координатами:

Определяя величину φ следует (по знакам х и у) определить

четверть, в которой лежит точка М, и учитывать, что – π < φ ≤ π.

Пример 1. Найти прямоугольные координаты точки М с полярными

координатами (2; – )

• Имеем r = 2, φ = – . x = r cos φ = 2 cos (– ) = 2 (– ) = –1,

y = r sin φ = 2 sin (– ) = 2 (– ) = – =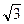> M (–1; – ).

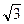Пример 2. Найти полярные координаты точки М с прямоугольными

координатами (– 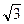; –1).

• Имеем x = – 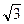, y = –1. r = = 2; tg φ = 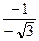= . Точка М лежит в III четверти, следовательно, с учетом того, что – π < φ ≤ π, получаем

φ = 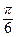– π = – 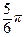=> M (2; – ).

---

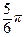Дата добавления: 2015-07-25