Расстояние d от точки М0 до плоскости

x cos α + y cos β + z cos γ – p = 0:

d = | х ₀cos α + у ₀cos β + z ₀cos γ – p |.

Пример 19. Составить уравнение плоскости, проходящей через точку

М (1, -3, -2) параллельно плоскости 3 x – 2 y + 4 z – 3 = 0.

• Ищем уравнение плоскости в виде Аx + Вy + Сz + D = 0. Две параллельные плоскости имеют общую нормаль. Координаты нормали заданной плоскости

n = { 3; –2; 4 }. Следовательно, уравнение искомой плоскости имеет вид

3 x – 2 y + 4 z + D = 0. Точка М (1, –3, –2 ) по условию лежит в искомой плоскости. Следовательно, подстановкой координат М в уравнение плоскости получим тождество: 3 × 1 – 2 × (–3) + 4 × (–2) + D = 0Þ D = –1Þ уравнение искомой плоскости имеет вид 3 x – 2 y + 4 z – 1 = 0.

Пример 20. Найти величину острого угла между плоскостями:

а) 11 х – 8 у – 7 z – 15 = 0 и 4 х – 10 у + z – 2 = 0;

б) 2 х + 3 у – 4 z + 4 = 0 и 5 х – 2 у + z – 3 = 0.

• а) cos φ = = =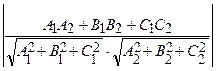

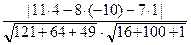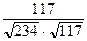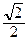= = => φ = .

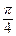б) выполняется условие перпендикулярности плоскостей A ₁ А ₂ + B ₁ B ₂ + C ₁ C ₂ = 0, т.к. 2 · 5 + 3 · (-2) – 4 · 1 = 0. Следовательно, плоскости взаимно перпендикулярны => φ = .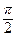

Пример 21. Написать уравнение плоскости, параллельной плоскости

х – 2 у + 2 z + 5 = 0 и удаленной от точки М (3, 4, -2) на расстояние d = 5.

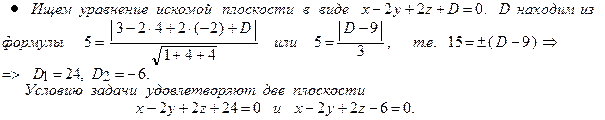
Пример 22. Составить уравнение плоскости, проходящей через точки

М ₁ (– 1, 3, 0) и М ₂ (2, 4, – 1), перпендикулярно плоскости х – 2 у + 3 z – 10 = 0.

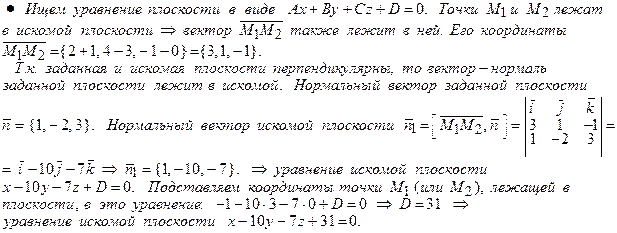
Дата добавления: 2015-07-25