Различные виды уравнения прямой в пространстве

1. Канонические уравнения прямой,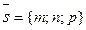

проходящей через данную точку (x ₀; у ₀; z ₀)

параллельно вектору 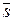= { m, n, p }:

Всякий ненулевой вектор, параллельный данной прямой, называется направляющим вектором этой прямой. Здесь направляющий вектор 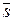= { m, n, p }. Обращение в нуль одного из знаменателей означает обращение в нуль числителя:

ó .

1. Параметрические уравнения прямой, проходящей через

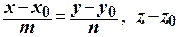данную точку (x ₀; у ₀; z ₀) параллельно вектору 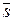= { m, n, p }:

,

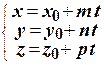где t – переменный параметр, t 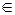R.

1. Уравнения прямой, проходящей через две точки

М ₁(x ₁; у ₁; z ₁) и М ₂(x ₂; у ₂; z ₂):

.

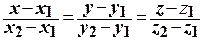4. Общее уравнение прямой 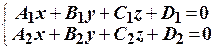задается как линия пересечения плоскостей А ₁ х + В ₁ у + С ₁ z + D ₁ = 0 и А ₂ х + В ₂ у + С ₂ z + D ₂ = 0.

Направляющий вектор этой прямой может быть найден как векторное произведение нормальных векторов = { A ₁; B ₁; С ₁} и

= { A ₂; B ₂; С ₂} этих плоскосте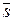й: = [ , ] или

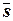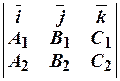= , т.е. = .

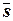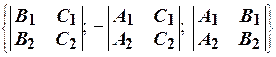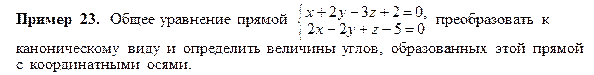
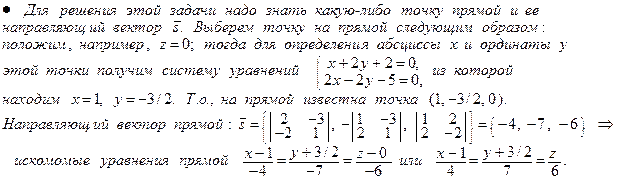
Замечание. Каноническое уравнение прямой можно получить, зная две точки этой прямой. В качестве этих точек можно взять два любых решения системы уравнений (общего уравнения прямой). Например, 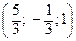и . Тогда уравнение прямой, проходящей через две точки, запишется в виде:

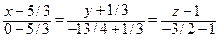, т.е. 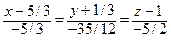, или .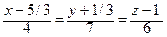

Направление прямой задает вектор 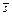= {4, 7, 6}. Он образует с координатными осями углы α, β и γ соответственно:

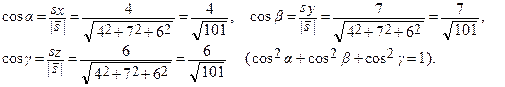
Дата добавления: 2015-07-25