директрисы.

Каноническое уравнение параболы: у ² = 2 рх, (5)

где р > 0 – параметр параболы – число, равное расстоянию от фокуса F до директрисы l.

Координаты фокуса: F (; 0). Точка О (0; 0) – вершина

параболы; длина r отрезка FM – фокальный радиус точки М; ось Ох

– ось симметрии параболы.

Уравнения директрисы l параболы: х = - . Фокальный радиус r = х + .

Парабола, симметричная относительно

оси Оу и проходящая через начало координат,

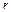
имеет уравнение: х ² = 2 ру. Ее фокусом

является точка F (0; ). Уравнения директрисы

у = - . Фокальный радиус r = у + .

Эскизы графиков других парабол:

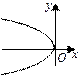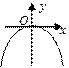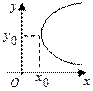у ² = -2 рх x ² = -2 рy (у – y ₀)² = 2 р (x – x ₀) ↑ (x – x ₀)² = 2 р (y – y ₀) ↑

(у – y ₀)² = -2 р (x – x ₀) х – x ₀)²=-2 р (y–y ₀)

Пример 14. Дана парабола х ² = 4 у. Найти координаты ее фокуса, уравнение

директрисы, длину фокального радиуса точки М (4; 4).

• Парабола задана каноническим уравнением. Следовательно, 2 р =4, р =2. Используя вышеприведенные формулы, находим, что фокус имеет координаты (0; 1), т.е. F (0; 1); уравнение директрисы имеет вид

у = –1; фокальный радиус точки М (4; 4) равен r = 4 + 1 = 5.

Пример 15. Найти вершину, фокус и директрису параболы у = –2 х ² + 8 х – 5,

построить эскиз графика.

• Приведем уравнение параболы к каноническому виду, выделив в правой части полный квадрат:

у = –2(х ² – 4 х + 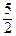) = –2(х ² – 4 х + 4 – 4 + 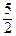) = –2((х – 2)² – ) = –2(х – 2)² + 3, т.е.

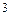
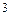
у = –2(х – 2)² + 3 или (х – 2² = – (у – 3).

Уравнение параболы имеет вид, как на рисунке. Вершина

параболы имеет координаты (2; 3); 2 р = , р = .

Прямая х = 2 является осью симметрии параболы.

Координаты фокуса х = 2, у = 3 – 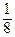= 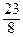, т.е. F (2; ).

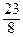Уравнение директрисы у = 3 + = 3 + 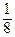, т.е. у = .

Пример 16. Найти уравнение касательной к параболе у ² = 4 х, проведенной из

точки А (–2; –1).

• Уравнение прямой ищем в виде y = kx + b. Т.к. точка А принадлежит искомой касательной, подставляя ее координаты в уравнение касательной, получим:

–1 = –2 k + b. Далее, эта прямая и парабола имеют единственную точку (касаются). Следовательно, система уравнений 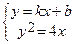имеет единственное решение. Решаем ее относительно х и у. Возведем правую и левую части первого уравнения в квадрат и подставим в левую часть полученного равенства вместо у ² его выражение из второго уравнения. Получим k ² x ² + 2 kbх + b ² = 4 x. Это – квадратное уравнение, имеющее единственное решение в случае, когда дискриминант равен нулю. Т.о., = (kb – 2)² – k ² b ² = 0 или 4 kb =4, b = . Искомые значения параметров k и b находятся как решения системы 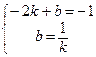, из которой получаем

–2 k ² + k + 1 = 0 и k ₁=1, k ₂=– . Система имеет два решения: 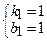и . Следовательно, две прямые удовлетворяют условиям задачи: y = x + 1 и y = – x –2.

Дата добавления: 2015-07-25