Читайте также:
|
Угол между прямой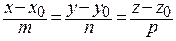 
и плоскостью
Ах + Ву + Сz + D = 0:
sin φ =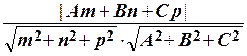 
.
Условие параллельности прямой и плоскости: Аm + Вn + Сp = 0.
Условие перпендикулярности прямой и плоскости: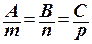 
.
Для нахождения точки пересечения прямой и плоскости удобно воспользоваться параметрическими уравнениями прямой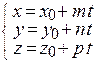 
. Подставив х, у и z в уравнение плоскости
А (х 0 + m t) + В (y 0 + n t)+ С (z 0 + p t)+ D = 0, находим значение t = tр. Координаты точки пересечения: .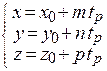 
.
Условие, при котором прямая лежит в плоскости:
.
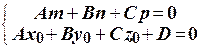Если Аm + Вn + Сp ≠ 0, то прямая пересекает плоскость;
если Аm + Вn + Сp = 0 и Ах 0 + Вy 0 + Сz 0 + D ≠ 0 – прямая параллельна плоскости.
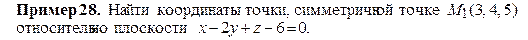
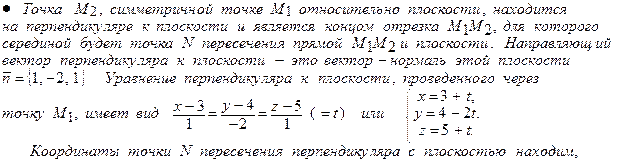решая систему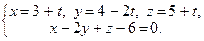 
Из равенства (3 + t) – 2(4 – 2 t) + (5 + t) – 6 = 0 вытекает равенство 6 t – 6 = 0,
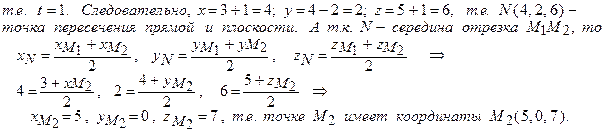
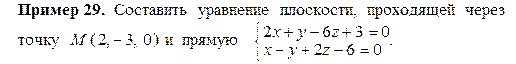
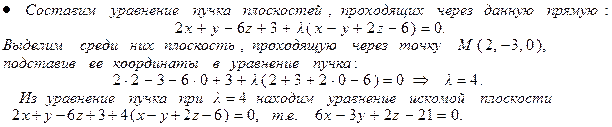
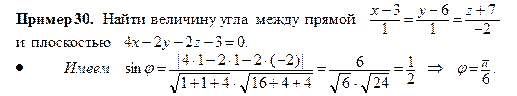
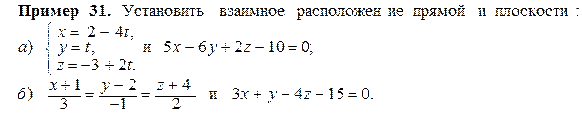
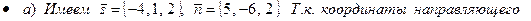вектора 
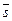прямой и нормального вектора 
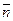плоскости не пропорциональны, то прямая не перпендикулярна плоскости.
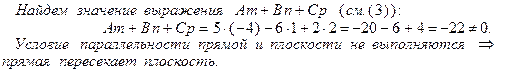
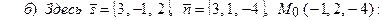
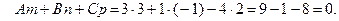
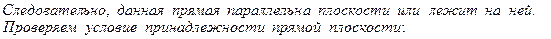
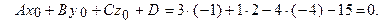
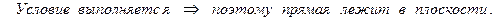
Линии, определяемые уравнениями
Ax 2 + 2 Bxy + Cy 2 + 2 Dx + 2 Ey + F = 0, (1)
называются кривыми второго порядка. Данное уравнение определяет на плоскости окружность, эллипс, гиперболу или параболу.
Дата добавления: 2015-07-25; просмотров: 49 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Прямые совпадают,когда и точка (x1; у1; z1) L2 и, наоборот, точка (x2; у2; z2) L1. | | | Окружность |