Приложение определителей к решению систем линейных уравнений.

а) Система двух линейных уравнений с двумя неизвестными:

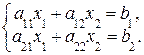(1.4)

Если 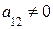, то выразим 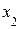из первого уравнения и подставим во второе:

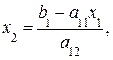
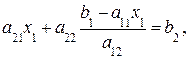
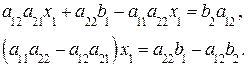
Положим 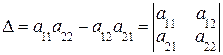, , 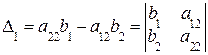и если 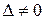, то . Аналогично, 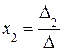, где .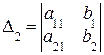

Определитель 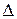называется определителем системы и при 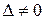решение системы (1.4) находим по формулам Крамера:

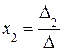, . (1.5)

б) Система трех линейных уравнений с тремя неизвестными:

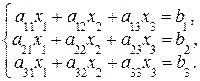(1.6)

Если определитель системы 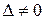, то система совместна и имеет единственное решение, которое находим по формулам Крамера:

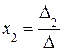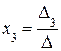, , , (1.7)

где ,

.

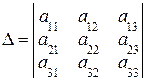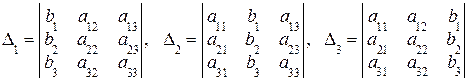Пример. Решить системы по формулам Крамера:

а) 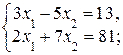б)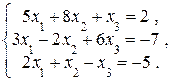

Решение. а)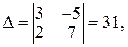

,

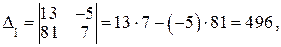
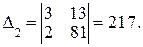
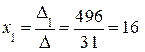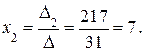
Ответ: (16;7).

б)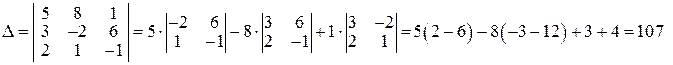

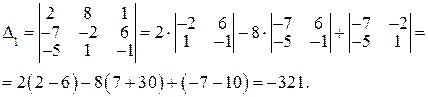
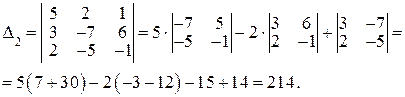
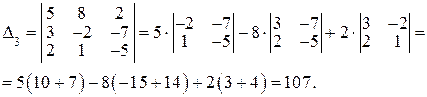
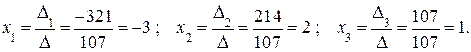
Ответ: (-3; 2; 1).

Дата добавления: 2015-07-20