Читайте также:
|
Рассмотрим задачи о нахождении расстояния между двумя точками и деления отрезка в данном отношении в пространстве.
Расстояние 
между двумя точками 
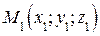и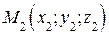 
равно длине диагонали прямоугольного параллелепипеда (см. рис. 2.4). Тогда
.
Если точка 
делит отрезок 
в отношении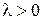 
, т. е. 
, то 
(2.5)
Если точка является серединой отрезка , то ее координаты получим из формул (2.5) при 
, т. е.
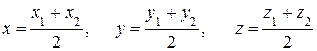. (2.6)
Дата добавления: 2015-07-20; просмотров: 70 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Декартовы координаты в пространстве. | | | Векторы на плоскости и в пространстве. |