Раздел 1. Элементы линейной алгебры и аналитической геометрии.

1. Определители.

Основные понятия.

Определение 1. Определителемвторогопорядка называется число

Δ= (1.1)

числа называются элементами определителя, где 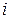- номер строки, 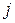- номер столбца; элементы 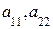образуют главную диагональ определителя; 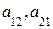– побочную диагональ. Поэтому определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.

Определение 2. Определителемтретьегопорядка называется число Δ= .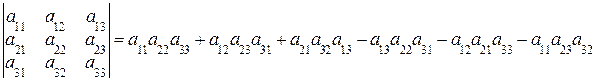

При вычислении определителя третьего порядка используется правило треугольников:

.

Элементы образуют главнуюдиагональ определителя; – побочнуюдиагональ.

Пример. Вычислить определитель

1) Δ= , 2) Δ= .

Решение:

1) Δ= ;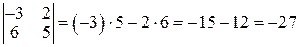

2)Δ= .

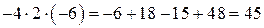Дата добавления: 2015-07-20