Основные задачи аналитической геометрии на плоскости.
ЧАСТЬ 1. Основной текст. | Раздел 1. Элементы линейной алгебры и аналитической геометрии. | Свойства определителей. | Приложение определителей к решению систем линейных уравнений. | Декартовы координаты в пространстве. | Основные задачи аналитической геометрии в пространстве. | Векторы на плоскости и в пространстве. | Линейные операции над векторами. | Координаты вектора в данном базисе. | Проекция вектора на ось. |
Расстояние между двумя точками.
Найдем расстояние d между точками  и
и 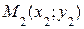 координатной плоскости
координатной плоскости
Оху (рис. 2.2 а). Это расстояние равно длине отрезка  , который является гипотенузой прямоугольного треугольника
, который является гипотенузой прямоугольного треугольника 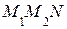 , и по теореме Пифагора
, и по теореме Пифагора
 (2.1)
(2.1)
Дата добавления: 2015-07-20; просмотров: 66 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.006 сек.)

 и
и 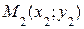 координатной плоскости
координатной плоскости
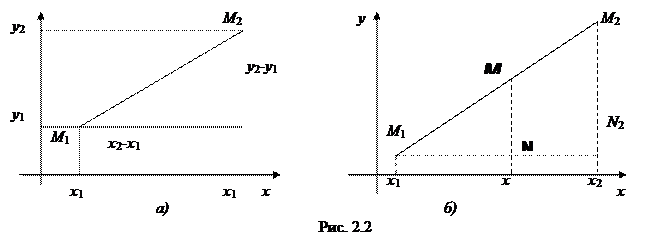
 , который является гипотенузой прямоугольного треугольника
, который является гипотенузой прямоугольного треугольника 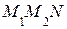 , и по теореме Пифагора
, и по теореме Пифагора
 (2.1)
(2.1)