Читайте также:
|
Рассмотрим на координатной плоскости Оху отрезок 
с концами в точках 
и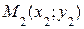 
(см. рис. 2.2 б).
Говорим, что точка М делит отрезок в отношении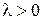 
, считая от точки 
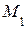, если 
. Найдем координаты точки 
, делящей отрезок в данном отношении 
, т. е. 
. Из рис. 2.2 б ясно, что
или 
.
Заметим, что левая часть последнего равенства положительна при любом следовании точек 
и 
на прямой, проходящей через точк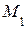и и 
.
Из последнего равенства получаем
, 
.
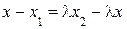Аналогично получаем 
.
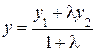Итак, мы нашли координаты точки , делящей отрезок в отношении :
. (2.2)
Из формул (2.2) при 
получим координаты середины отрезка :
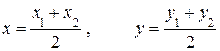(2.3)
Дата добавления: 2015-07-20; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Основные задачи аналитической геометрии на плоскости. | | | Декартовы координаты в пространстве. |