
Читайте также:
|
Пусть в пространстве задана числовая ось u, т.е. прямая с выбранным на ней направлением и масштабом.
Проекция точки М на ось u – это основание М1 перпендикуляра ММ1, опущенного из
точки М на ось. Для построения точки М1 проведем через точку М плоскость перпендикулярно оси, тогда точка М1 есть точка их пересечения (см. рис. 3.12).
Рассмотрим произвольный вектор  =
=  . Обозначим
. Обозначим  1=
1=  1 вектор, где А1 и В1 проекции на ось u соответственно начала А и конца В вектора
1 вектор, где А1 и В1 проекции на ось u соответственно начала А и конца В вектора  (см. рис. 3.13).
(см. рис. 3.13).
 |
 на ось u называется число |
на ось u называется число |  1|, если вектор
1|, если вектор  1 и ось u сонаправлены и число -|
1 и ось u сонаправлены и число -|  1|, ели вектор
1|, ели вектор  1 и ось u противоположно направлены.
1 и ось u противоположно направлены.
Проекция вектора  на ось u обозначается так: ПР u
на ось u обозначается так: ПР u  . Иными словами:
. Иными словами:
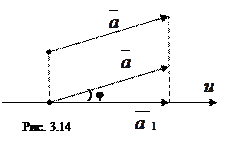 ПР u
ПР u  =
= 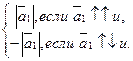
Обозначим через φ угол между вектором  и осью u (см. рис. 3.14), ясно, что 0≤φ≤π. Тогда ПР u
и осью u (см. рис. 3.14), ясно, что 0≤φ≤π. Тогда ПР u  =
=  .
.
Заметим что ПР u  >0 ó 0≤φ<
>0 ó 0≤φ< 
и ПР u  <0, ó 0≤φ<
<0, ó 0≤φ<  .
.
Основные свойства проекций векторов на ось.
a) 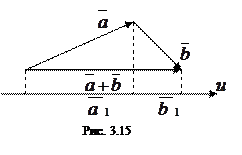 Проекция суммы векторов на ось равна сумме проекций этих векторов на ту же ось (см. рис. 3.15):
Проекция суммы векторов на ось равна сумме проекций этих векторов на ту же ось (см. рис. 3.15):
ПР u ( +
+  )= ПР u
)= ПР u  + ПР u
+ ПР u 
Из рис. 3.15 ясно, что ПР u ( +
+  )=|
)=|  1|+|
1|+|  1|= ПР u
1|= ПР u  +
+
+ ПР u 
b) При уменьшении вектора  на число λ его проекция на ось также умножается на число λ:
на число λ его проекция на ось также умножается на число λ:
ПР u (λ  )=λ ПР u
)=λ ПР u  .
.
Действительно, если λ>0, то ПР u (λ  ) = |λ
) = |λ  |
|  = λ|
= λ|  |
|  = λ ПР u
= λ ПР u  .
.
Если λ<0, то (см. рис. 3.16) ПР u (λ  )=|λ
)=|λ  |•
|•  = -λ|
= -λ|  |(-
|(-  )=λ|
)=λ|  |
|  = λ ПР u
= λ ПР u  .
.
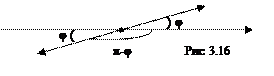 Из свойств 1 и 2 вытекает, что
Из свойств 1 и 2 вытекает, что
ПР u (α  +β
+β  )=α ПР u
)=α ПР u  +β ПР u
+β ПР u  ,
,
т.е. проекция линейной комбинации векторов равна соответствующей линейной комбинации их проекций.
Дата добавления: 2015-07-20; просмотров: 73 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Координаты вектора в данном базисе. | | | Ортонормированный базис на плоскости и в пространстве. |