
Читайте также:
|
a) Рассмотрим на плоскости декартову прямоугольную систему координат Оху.
Выберем на координатных осях Ох и Оу единичные векторы (орты)  и
и  соответственно:
соответственно:
|  | = |
| = |  | = 1 и
| = 1 и 

 (см. рис. 3.17). Векторы
(см. рис. 3.17). Векторы  и
и  образуют базис плоскости. Такой базис называется ортонормированным.
образуют базис плоскости. Такой базис называется ортонормированным.
Для каждого вектора  плоскости
плоскости  ,
,  :
:
 = х
= х  + у
+ у  ={ х,у } (3.3)
={ х,у } (3.3)
 Если начало вектора
Если начало вектора  совместить сточкой О (см. рис. 3.17), то становится ясно, что координаты х и у вектора
совместить сточкой О (см. рис. 3.17), то становится ясно, что координаты х и у вектора  в базисе
в базисе  и
и  есть не что иное, как проекции вектора на соответствующие оси координат:
есть не что иное, как проекции вектора на соответствующие оси координат:
х=ПРх  , у=ПРу
, у=ПРу 
Координаты х и у называются декартовыми координатами вектора  . Ясно также, что
. Ясно также, что
|  |=
|= 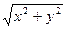 ,
,
т.е. модуль (длина) вектора в ортонормированном базисе  ,
,  равен квадратному корню из суммы квадратов его координат.
равен квадратному корню из суммы квадратов его координат.
Обозначим через α и β углы, образованные вектором  с осями Ох и Оу соответственно (см. рис. 3.17), тогда
с осями Ох и Оу соответственно (см. рис. 3.17), тогда
х=|  | соs α, у= |а|соs β, или соs α=
| соs α, у= |а|соs β, или соs α= 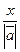 , соs β=
, соs β= 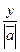 .
.
Числа соs α и соs β называются направляющими косинусами вектора  . Они обладают свойством:
. Они обладают свойством:
 .
.
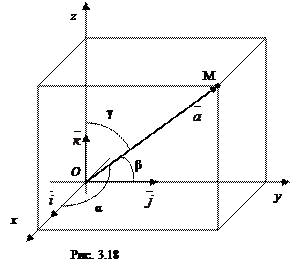
б) Рассмотрим в пространстве декартову прямоугольную систему координат Охуz. Выберем на координатных осях Ох, Оу и Оz координатные орты  ,
,  ,
, 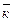 соответственно (см. рис. 3.18), при этом |
соответственно (см. рис. 3.18), при этом |  | = |
| = |  | = |
| = |  | = 1 и эти векторы попарно ортогональны, т.е. образуют ортонормированный базис пространства. Аналогично плоскому случаю, для любого
| = 1 и эти векторы попарно ортогональны, т.е. образуют ортонормированный базис пространства. Аналогично плоскому случаю, для любого  справедливо разложение
справедливо разложение
 = х
= х  + у
+ у  + z
+ z  ={ х,у,z }, (3.4)
={ х,у,z }, (3.4)
где х, у, z – координаты вектора  в базисе из векторов
в базисе из векторов  ,
,  ,
,  , при этом
, при этом
х=ПРх  , у=ПРу
, у=ПРу  , z =ПРz
, z =ПРz  ,
,
|  |=
|=  .
.
Если α, β, γ – углы, образованные вектором  с соответствующими осями координат, то
с соответствующими осями координат, то
соs α =  , соs β =
, соs β =  , соs γ =
, соs γ =  .
.
Числа соs α, соs β, соs γ – направляющие косинусы вектора  и
и
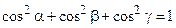 .
.
Дата добавления: 2015-07-20; просмотров: 150 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Проекция вектора на ось. | | | Действия над векторами в координатной форме. |