
|
Читайте также: |
Рассмотрим одно из основных понятий линейной алгебры – понятие базиса линейного пространства.
Упорядоченная система векторов е 1, …, еn называется базисом линейного пространства L, если выполняются условия:
1) эта система векторов линейно независима,
2) каждый вектор х Î L является линейной комбинацией векторов этой системы.
Итак, если система векторов е= { е 1, …, еn } базис в L, то каждый вектор х Î L разлагается в линейную комбинацию базисных векторов, т.е. существуют числа a 1, …, an Î R такие, что
x=a 1 х 1+ a 2 х 2+ …+ anxn. (6.2)
Числа a 1, a 2, …, an в разложении (6.2) вектора х по базису е= { е 1, …, еn } называется координатами вектора х в базисе е: х =(a 1, a 2, …, an)e.
Теорема 6.3. Пусть е= { е 1, …, еn }- базис линейного пространства L, х,у Î L и
x=a 1 е 1+…+ anеn =(a 1,…, an)e, у=b 1 е 1+…+ bnеn =(b 1,…, bn)e. Тогда справедливы утверждения:
1) координаты вектора определяются единственным образом,
2) при сложении векторов их соответствующие координаты складываются:
х+у= (a 1+ b 1) е 1+…+(an + bn) еn =(a 1+ b 1,…, an+bn)e,
3) при умножении вектора х на число l каждая координата х умножается на число l:
x= (la 1 е 1)+…+(lanеn)=(l a 1,…, lan)e.
Доказательство. 1. Допустим, что это не верно, т.е. существуют два разложения вектора х по базису е:
x=a 1 е 1+…+ anеn и х=b 1 е 1+…+ bnеn.
Вычитая эти равенства, на основании аксиом 1, 2 и 8 получим
θ=х - х=a 1 е 1+…+ anеn - b 1 е 1-…- bnеn. = (a 1- b 1) е 1+…+(an - bn) еn.
Так как система векторов е 1, …, еn линейно независима то a 1- b 1=0, …, an - bn =0, т.е. a 1= b 1, …, an = bn.
Итак, координаты вектора в данном базисе определяются однозначно и, тем самым, полностью характеризуют вектор в этом базисе.
Свойства 2 и 3 представляют собой действия над векторами в координатной форме и вытекают непосредственно из аксиом линейного пространства (предлагается проверить самостоятельно).
Размерность линейного пространства. Линейное пространство L называется n -мерным или пространством размерности n, если в нем существует базис из n векторов.
Покажем, что определение размерности корректно, т.е. что все базисы линейного пространства имеют одно и то же число векторов, равное размерности пространства.
Теорема 6.4. Пусть L – n -мерное линейное пространство. Тогда справедливы утверждения:
1) любые n +1 векторов этого пространства линейно зависимы;
2) любые n линейно независимых векторов из L образуют его базис.
Доказательство: 1) L – n -мерное линейное пространство, т.е. в нем существует базис из n векторов е= { е 1, …, еn }. Доказательство проведем методом от противного. Пусть существует в L линейно независимая система из (n +1)-го вектора х 1, …, xn+ 1.
Рассмотрим систему векторов х1, е1, …, еn, которая линейно зависима, т.к. е= { е 1, …, еn } – базис пространства, поэтому х1 есть линейная комбинация векторов е1, …, еn:
x=a 1 е 1+ a 2 е 2+…+ anеn, (6.3)
и, так как х1 ¹ θ, один из коэффициентов a 1,…, an отличен от нуля. Пусть, например, α 1¹0, тогда
е 1= – 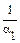 х 1 –
х 1 –  е 2 –…–
е 2 –…– 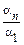 еn. (6.4)
еn. (6.4)
Система векторов х1, е2, …, еn линейно независима. Если бы она была линейно зависима, то вектор х1 разлагался по векторам е2, …, еn, которые линейно независимы. Это противоречит единственности разделения по базису (6.3), где α 1¹0.
Покажем, что каждый вектор х Î L является линейный комбинацией векторов х1, е2, …, еn. Действительно, каждый вектор х Î L является линейной комбинаций векторов базиса е1, …, еn:
х=b 1 е 1+ b 2 е 2+…+ bnеn.
Заменяя в последнем равенстве вектор е 1 по формуле (6.4) мы получим вектор х как линейную комбинацию векторов х1, е2, …, еn. Итак, векторы х1, е2, …, еn образуют базис в L.
Продолжая эту процедуру, мы векторы е1, …, еn исходного базиса заменим последовательно на векторы х 1, …, xn, получая на каждом шаге базис пространства L. После n шагов мы получим базис, состоящий из векторов х 1, …, xn. Тогда вектор хn +1 должен быть линейной комбинацией векторов х 1, …, xn, что противоречит линейной независимости векторов х 1, …, xn, xn +1. Это противоречие доказывает первое утверждение теоремы.
Второе утверждение теоремы сразу вытекает из первого.
Доказательство теоремы закончено.
Базисом системы векторов х 1, …, xm называется такая ее часть 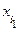 , …,
, …,  , к £ m и 1£ i 1< i 2<…< ik £ m, которая удовлетворяет следующим условиям:
, к £ m и 1£ i 1< i 2<…< ik £ m, которая удовлетворяет следующим условиям:
1) 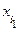 , …,
, …,  - линейно независимая система векторов,
- линейно независимая система векторов,
2) каждый вектор системы х 1, …, хm называется линейной комбинацией векторов
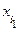 , …,
, …,  .
.
Рангом системы векторов х 1, …, xm называется максимальное число линейно независимых векторов этой системы и обозначается r (x 1, …, xm).
Все базисы данной системы векторов имеют одинаковое число векторов, равное рангу этой системы.
Пример 6.1. Рассмотрим множество геометрических векторов в пространстве, определенных в п. 3.1., с линейными операциями сложения векторов и умножения вектора на число, определенных в пункте 3.2. Как показывают свойства этих операций, множество геометрических векторов в пространстве является векторным пространством над полем R действительных чисел. Обозначим его V3.
Линейная зависимость двух векторов из V3 равносильна их коллинеарности. Линейная зависимость трех векторов равносильна их компланарности.
Базис пространства V3 образуют любые три ненулевых некомпланарных вектора. Поэтому это пространство трехмерно.
6.4. Пространство арифметических векторов Rn.
Арифметическим n -мерным вектором  называется упорядоченный набор из n действительных чисел а 1, а 2, …, аn, который записывается в виде
называется упорядоченный набор из n действительных чисел а 1, а 2, …, аn, который записывается в виде
 =(а 1, а 2, …, аn).
=(а 1, а 2, …, аn).
числа а 1, а 2, …, аn называются компонентами вектора  .
.
Два n -мерных вектора  =(а 1,…, аn) и
=(а 1,…, аn) и  =(b 1,…, bn) называются равными,
=(b 1,…, bn) называются равными,  =
=  , если равны их соответствующие компоненты: а 1= b 1,…, аn = bn.
, если равны их соответствующие компоненты: а 1= b 1,…, аn = bn.
Нулевой вектор  – это вектор, все компоненты которого равны нулю:
– это вектор, все компоненты которого равны нулю:  = (0, 0, …, 0).
= (0, 0, …, 0).
Вектор -  =(- а 1, - а 2, …, - аn) называется противоположным вектору
=(- а 1, - а 2, …, - аn) называется противоположным вектору  =(а 1, а 2, …, аn).
=(а 1, а 2, …, аn).
Суммой двух n -мерных векторов  =(а 1,…, аn) и
=(а 1,…, аn) и  =(b 1,…, bn) называется n -мерный вектор
=(b 1,…, bn) называется n -мерный вектор
 +
+  =(а 1+ b 1, а 2+ b 2,…, аn + bn), (6.5)
=(а 1+ b 1, а 2+ b 2,…, аn + bn), (6.5)
т.е. при сложении двух n -мерных векторов их соответствующие компоненты складываются.
Произведением n -мерного вектора  =(а 1, а 2, …, аn) на действительное число l называется n -мерный вектор
=(а 1, а 2, …, аn) на действительное число l называется n -мерный вектор
l  =(l а 1, l а 2, …, l аn), (6.6)
=(l а 1, l а 2, …, l аn), (6.6)
т.е. при умножении вектора на число каждая компонента вектора умножается на это число. В частности,
-  =(-1)
=(-1)  .
.
Так определенные операции над арифметическими n -мерными векторами удовлетворяют всем аксиомам линейного (векторного) пространства. Итак, множество всех арифметических n -мерных векторов с введенными выше операциями сложения векторов и умножения вектора на число образует векторное пространство над полем R действительных чисел, обозначают его Rn и называют пространством арифметических векторов.
Рассмотрим в Rn систему векторов 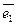 ,
, 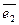 , …,
, …, 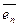 вида:
вида:
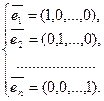 (6.7)
(6.7)
Покажем, что эта система векторов образует базис пространства Rn, называемый стандартным базисом в Rn. Для этого покажем, что эта система векторов линейно независима и каждый вектор из Rn является линейной комбинацией векторов этой системы.
Пусть числа α1, α2, …, α n таковы, что α1 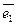 + α2
+ α2 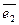 + +α n
+ +α n 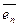 =
= 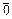 . Учитывая правила сложения векторов и умножения вектора на число в Rn, получим
. Учитывая правила сложения векторов и умножения вектора на число в Rn, получим
(a 1, a 2, …, an) =(0, 0, …, 0),
т.е. a 1=0, a 2=0, …, an =0. Это означает, что векторы 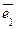 ,
, 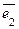 , …,
, …, 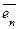 линейно независимы. Далее
линейно независимы. Далее
 =(а 1, а 2, …, аn) = (а 1, 0, …, 0) + (0, а 2, …, 0) + (0, 0, …, аn)=
=(а 1, а 2, …, аn) = (а 1, 0, …, 0) + (0, а 2, …, 0) + (0, 0, …, аn)=
= a1 (1, 0, …, 0) + a2 (0, 1, …, 0) + an (0, 0, …, 1)= a1 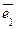 + a2
+ a2 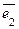 +…+ an
+…+ an 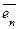 ,
,
т.е. каждый вектор  Î Rn есть линейная комбинация векторов системы
Î Rn есть линейная комбинация векторов системы 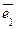 ,
, 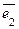 , …,
, …, 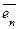 .
.
Теперь ясно, что компоненты a1, a2,,an вектора ā = (a1, a2, …, an)Î Rn есть не что иное, как координаты вектора ā в стандартном базисе. Пространство Rn является n -мерным векторным пространством.
Пример 6.2. Рассмотрим линейное пространство геометрических векторов V 3, определенное в параграфе 3 (см. п. 3.1, 3.2) и ортонормированный базис из векторов 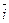 ,
,  ,
, 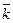 (см. п.3.5 б). Тогда каждый вектор ā Î V 3 единственным образом разлагается по базису
(см. п.3.5 б). Тогда каждый вектор ā Î V 3 единственным образом разлагается по базису 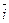 ,
,  ,
, 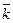 :
:
ā=х 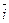 + у
+ у  + z
+ z 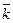 = { х, у, z },
= { х, у, z },
где числа х, у, z - координаты вектора ā в данном базисе. Упорядоченная тройка чисел { х, у, z } однозначно характеризует вектор ā. Сложению векторов и умножению вектора на число соответствуют аналогичные действия над их координатами (см. п. 3.6).
Таким образом, мы установили взаимно однозначное соответствие между векторами пространства V 3 и упорядоченными тройками их координат (в базисе 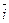 ,
,  ,
, 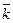 ), сохраняющее линейные операции сложения векторов и умножения вектора на число. Но упорядоченная тройка чисел есть не что иное, как трехмерный арифметический вектор из R 3:
), сохраняющее линейные операции сложения векторов и умножения вектора на число. Но упорядоченная тройка чисел есть не что иное, как трехмерный арифметический вектор из R 3:
ā=х 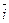 + у
+ у  + z
+ z 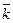 ={ х, у, z } ó (х, у, z) Î R 3
={ х, у, z } ó (х, у, z) Î R 3
Заметим, что ортонормированному базису 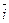 ,
,  ,
, 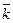 в V 3 соответствует стандартный базис
в V 3 соответствует стандартный базис 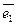 ,
, 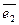 ,
, 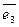 в R 3:
в R 3:
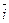 =1•
=1• 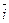 + 0•
+ 0•  + 0•
+ 0• 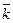 ={1, 0, 0} ó
={1, 0, 0} ó 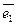 =(1, 0, 0),
=(1, 0, 0),
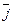 =0•
=0• 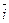 + 1•
+ 1•  + 0•
+ 0• 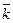 ={0, 1, 0} ó
={0, 1, 0} ó 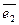 =(0, 1, 0),
=(0, 1, 0),
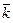 =0•
=0• 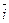 + 0•
+ 0•  + 1•
+ 1• 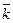 ={0, 0, 1} ó
={0, 0, 1} ó 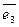 =(0, 0, 1).
=(0, 0, 1).
Тогда пространство геометрических векторов V 3 можно рассматривать как конкретную реализацию векторного пространства арифметических векторов R 3.
Пример 6.3. Пусть векторы 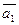 ,
, 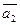 , …,
, …, 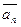 образуют базис пространства Rn, в частности, они линейно независимы, т.е. равенство
образуют базис пространства Rn, в частности, они линейно независимы, т.е. равенство
α1 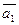 + α2
+ α2 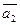 +, …, + α n
+, …, + α n 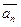 =
=  (6.7)
(6.7)
выполняется тогда и только тогда, когда α1=0, α2=0, …, α n =0.
Пусть векторы 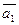 ,
, 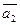 , …,
, …, 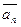 заданы своими координатами:
заданы своими координатами:
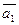 =(а 11, а 21, …, аn 1),
=(а 11, а 21, …, аn 1),
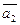 =(а 12, а 22, …, аn 2),
=(а 12, а 22, …, аn 2),
……………………..
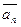 =(а 1 n, а 2 n, …, аnn).
=(а 1 n, а 2 n, …, аnn).
Перепишем равенство (6.7) в координатной форме:
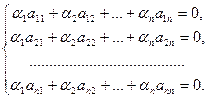 (6.8)
(6.8)
Эта система n линейных уравнений с n неизвестными, однородная: она совместна и имеет решение α1=0, α2=0, …, α n =0. Если определитель этой системы
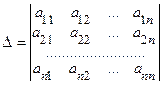 (6.9)
(6.9)
отличен от нуля, ∆≠0, то решение системы (6.8) единственно.
Итак, векторы 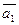 ,
, 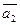 , …,
, …, 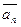 образуют базис Rn тогда и только тогда, когда определитель, составленный из координат этих векторов, отличен от нуля.
образуют базис Rn тогда и только тогда, когда определитель, составленный из координат этих векторов, отличен от нуля.
Если этот определитель равен нулю, ∆=0, то система векторов линейно зависима и один из векторов этой системы является линейной комбинацией остальных.
Скалярным произведением двух векторов  =(а 1, а 2,…, аn) и
=(а 1, а 2,…, аn) и  =(b 1, b 2,…, bn) из Rn называется число
=(b 1, b 2,…, bn) из Rn называется число
( ,
,  ) = а 1 b 1 + а 2 b 2+… + аnbn. (6.10)
) = а 1 b 1 + а 2 b 2+… + аnbn. (6.10)
Основные свойства скалярного произведения:
1. ( ,
,  )=(
)=( ,
,  ).
).
2. (a  ,
,  )= (
)= ( , a
, a  )= a (
)= a ( ,
,  ).
).
3. ( +
+  ,
, 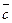 )=(
)=( ,
, 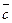 )+(
)+( ,
, 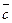 ).
).
4. ( ,
,  )³0, (
)³0, ( ,
,  )=0 ó
)=0 ó  =0
=0
Эти свойства вытекают непосредственно из определения скалярного произведения по формуле (6.10).
Модулем ( длиной ) вектора  =(а 1, а 2,…, аn) Î Rn называется число
=(а 1, а 2,…, аn) Î Rn называется число
|  |=
|= 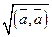 =
= 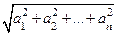 . (6.11)
. (6.11)
Угол между ненулевыми векторами  и
и  из Rn называется угол j= (
из Rn называется угол j= (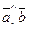 ), 0£j£p такой, что
), 0£j£p такой, что
cos j= 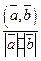 . (6.12)
. (6.12)
Векторы  и
и  называются ортогональными,
называются ортогональными,  ^
^  , если(
, если(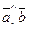 )=j=
)=j= 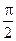 , т.е. если их скалярное произведение равно нулю:
, т.е. если их скалярное произведение равно нулю:
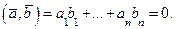
Пространство векторов Rn со скалярным произведением, заданным формулой (6.10), называется евклидовым пространством Rn.
Базис пространства называется ортонормированным, если векторы, образующие базис, попарно ортогональны и имеют длину, равную единице, т.е. являются ортами:
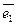 ,
, 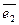 , …,
, …, 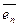 – ортонормированный базис Rn ó
– ортонормированный базис Rn ó 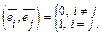
Так стандартный базис в Rn (см. 6.7) является ортонормированным базисом в Rn.
Пример 6.4. Пространство V 3 со скалярным произведением, определенным в п. 4.1., является трехмерным евклидовым пространством, а векторы 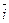 ,
,  ,
, 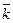 (координатные орты) образуют ортонормированный базис V 3.
(координатные орты) образуют ортонормированный базис V 3.
Дата добавления: 2015-07-20; просмотров: 142 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Линейная зависимость | | | Понятие уравнения линии на плоскости. |