
Читайте также:
|
1) Угол между векторами.
Пусть даны два ненулевых вектора  ={ х1, у1, z1 } и
={ х1, у1, z1 } и  ={ х2, у2, z2 }, φ=(
={ х2, у2, z2 }, φ=( ,^
,^  ) – угол между ними. Тогда
) – угол между ними. Тогда
 . (4.6)
. (4.6)
2) Условие ортогональности векторов.
Два ненулевых вектора  и
и  ортогональны, если φ = (
ортогональны, если φ = ( ,^
,^  ) = π/2 (90°). Тогда из определения скалярного произведения следует (см. формулу (4.1)), что
) = π/2 (90°). Тогда из определения скалярного произведения следует (см. формулу (4.1)), что 

 ó
ó 
 = 0, или в координатной форме
= 0, или в координатной форме


 ó х1х2 + у1у2 + z1z2=0.
ó х1х2 + у1у2 + z1z2=0.
3) Проекция вектора на заданное направление.
Найдем проекцию вектора  на направление, заданное вектором
на направление, заданное вектором  из равенства (4.2):
из равенства (4.2):
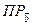
 =
=  , где
, где  – орт вектора
– орт вектора  , или в координатной форме
, или в координатной форме
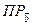
 =
= 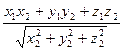 .
.
Дата добавления: 2015-07-20; просмотров: 84 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Скалярное произведение в координатной форме. | | | Определение векторного произведения. |