Глава 2. Теория сравнений с арифметическими приложениями.

Теория чисел имеет свою алгебру, известную, как теория сравнений. Обычная алгебра первоначально развивалась как стенография для операций арифметики. Аналогично, сравнения представляют собой символический язык для делимости, основного понятия теории чисел.

Понятие сравнения было введено впервые Гауссом в «Disquisitiones Arithmeticae». Это понятие фактически в неявном виде употреблялось многими математиками до Гаусса, однако только Гаусс точно определил его и систематически развил соответствующую теорию. Дальнейшие, фундаментальные результаты Гаусса, изложенные в этой книге, из которых особенно надо выделить квадратичный закон взаимности, явились основой всего последующего развития теории чисел. Метод сравнений, созданный Гауссом и лежащий в основе теории сравнений, является по существу формальным методом. Однако этот метод весьма полезен в техническом отношении. Он полезен как инструмент, с помощью которого можно в целом ряде случаев довольно легко получать такие результаты, подход к которым с помощью иных методов представляется громоздким.

§ 1. Сравнения в кольце целых чисел. Системы вычетов.

1. Отношение сравнимости, свойства.

Определение 1. Пусть . Целые числа 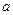и 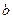называют сравнимыми по модулю , если . Обозначение: .

Примеры. .

Теорема 1. тогда и только тогда, когда 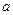и 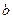при делении на имеют равные остатки, то есть являются равноостаточными.

Доказательство. По теореме о делении с остатком получаем , , . Тогда , по свойствам делимости из последнего соотношения вытекает утверждение теоремы.

Дата добавления: 2015-07-20